
【题目】已知 n 个四元集合 A1 , A2 ,…, An ,每两个有且只有一个公共元 ,并且有Card(A1 ∪ A2 ∪ …∪ An)=n .试求 n 的最大值.这里 Card A 为集合A中元素的个数 .
【答案】13
【解析】
考虑任一元![]() .
.
如果每个 Ai 均含有a , 则由条件知, 各 Ai 中的其他元素都不相同.
故![]() ,与已知条件相违.
,与已知条件相违.
因此, 必有一个 Ai 不含a .
不妨设 a![]() A1 .若含 a 的集合大于或等于 5个, 那么, 由已知条件得知 A1与这 5个集合各有一个公共元(此元当然不等于a), 而且这 5个元互不相同(若相同, 则这个公共元是2个含 a 的集合的公共元 , 于是, 这两个集合就有 2 个公共元, 又与已知条件相违), 从而, Card A1≥5, 矛盾.所以 , 含a的集合小于或等于 4 个.
A1 .若含 a 的集合大于或等于 5个, 那么, 由已知条件得知 A1与这 5个集合各有一个公共元(此元当然不等于a), 而且这 5个元互不相同(若相同, 则这个公共元是2个含 a 的集合的公共元 , 于是, 这两个集合就有 2 个公共元, 又与已知条件相违), 从而, Card A1≥5, 矛盾.所以 , 含a的集合小于或等于 4 个.
另一方面, 因为![]() ,所以, 每个元恰好属于 4个集合.
,所以, 每个元恰好属于 4个集合.
不妨设含有元 b 的集合为 A1 、A2 、A3 、A4.
由上述的结论可知![]() .
.
如果 n >13, 那么, 存在元 c![]() A1∪A2∪A3∪A4.设含 c 的集合为 A5, 则 A5不是
A1∪A2∪A3∪A4.设含 c 的集合为 A5, 则 A5不是![]() .因而, 不含 b .而 A5与
.因而, 不含 b .而 A5与![]() 各有一个公共元(当然不是 b), 这 4个公共元互不相同(理由同上), 又都不是 c , 从而,
各有一个公共元(当然不是 b), 这 4个公共元互不相同(理由同上), 又都不是 c , 从而,![]() , 矛盾.
, 矛盾.
因此, n ≤13.
n ≤13 是可能的.例如, 不难验证, 如下的13个集合符合要求.
{0, 1, 2, 3},{0, 4, 5, 6},{0, 7, 8, 9},{0, 10, 11, 12},{10, 1, 4, 7}, {10, 2, 5, 8}, {10, 3, 6, 9},{11, 1, 5, 9},{11, 2, 6, 7}, {11, 3, 4, 8}, {12, 1, 6, 8},{12, 2, 4, 9},{12, 3, 5, 7}.
故 n 的最大值为13.


科目:高中数学 来源: 题型:
【题目】将函数![]() 图象上所有点的横坐标缩短为原来的
图象上所有点的横坐标缩短为原来的![]() ,纵坐标不变,再向右平移
,纵坐标不变,再向右平移![]() 个单位长度,得到函数
个单位长度,得到函数![]() 的图象,则下列说法正确的是( )
的图象,则下列说法正确的是( )
A. 函数![]() 的一条对称轴是
的一条对称轴是![]()
B. 函数![]() 的一个对称中心是
的一个对称中心是![]()
C. 函数![]() 的一条对称轴是
的一条对称轴是![]()
D. 函数![]() 的一个对称中心是
的一个对称中心是![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两人参加某电视台举办的答题闯关游戏,按照规则:每人从备选的10道题中一次性抽取3道题独立作答,至少答对2道题即闯关成功.已知10道备选题中,甲只能答对其中的6道题,乙答对每道题的概率都是![]() .
.
(Ⅰ)求甲闯关成功的概率;
(Ⅱ)设乙答对题目的个数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下图是我国2010年至2016年生活垃圾无害化处理量(单位:亿吨)的折线图

注:年份代码1~7分别对应年份2010~2016
(1)由折线图看出,可用线性回归模型拟合y与t的关系,请求出相关系数r,并用相关系数的大小说明y与t相关性的强弱;
(2)建立y关于t的回归方程(系数精确到0.01),预测2018年我国生活垃圾无害化处理量.
附注:
参考数据:![]() ,
,![]() ,
,![]() ,
, ![]() .
.
参考公式:
相关系数
回归方程![]() 中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为:

![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】高血压高血糖和高血脂统称“三高”.如图是西南某地区从2010年至2016年患“三高”人数y(单位:千人)的折线图.
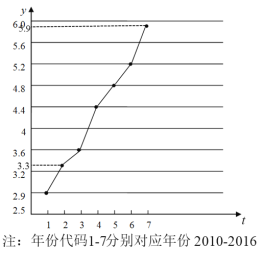
(1)由折线图看出,可用线性回归模型拟合![]() 与
与![]() 的关系,请求出相关系数(精确到0.01)并加以说明;
的关系,请求出相关系数(精确到0.01)并加以说明;
(2)建立![]() 关于
关于![]() 的回归方程,预测2018年该地区患“三高”的人数.
的回归方程,预测2018年该地区患“三高”的人数.
参考数据:![]() ,
,![]() ,
,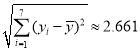 ,
,![]() .参考公式:相关系数
.参考公式:相关系数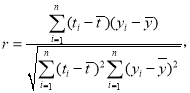 回归方程
回归方程![]() 中斜率和截距的最小二乘法估计公式分别为:
中斜率和截距的最小二乘法估计公式分别为:
![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com