
【题目】已知函数![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 在
在![]() 上的值域;
上的值域;
(2)若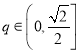 ,函数
,函数![]() 在
在![]() 上的最大值是
上的最大值是![]() ,求
,求![]() 的取值范围;
的取值范围;
(3)若不等式![]() 在
在![]() 上恒成立,求实数
上恒成立,求实数![]() 的取值范围.
的取值范围.
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() ,
,![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系,直线
轴正半轴为极轴建立极坐标系,直线![]() 的坐标方程为
的坐标方程为![]() ,若直线
,若直线![]() 与曲线
与曲线![]() 相切.
相切.
(1)求曲线![]() 的极坐标方程;
的极坐标方程;
(2)在曲线![]() 上取两点
上取两点![]() 、
、![]() 于原点
于原点![]() 构成
构成![]() ,且满足
,且满足![]() ,求面积
,求面积![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分13分)
某产品按行业生产标准分成8个等级,等级系数X依次为1,2,……,8,其中X≥5为标准A,X≥3为标准B,已知甲厂执行标准A生产该产品,产品的零售价为6元/件;乙厂执行标准B生产该产品,产品的零售价为4元/件,假定甲、乙两厂得产品都符合相应的执行标准
(I)已知甲厂产品的等级系数X1的概率分布列如下所示:

且X1的数字期望EX1=6,求a,b的值;
(II)为分析乙厂产品的等级系数X2,从该厂生产的产品中随机抽取30件,相应的等级系数组成一个样本,数据如下:
3 5 3 3 8 5 5 6 3 4
6 3 4 7 5 3 4 8 5 3
8 3 4 3 4 4 7 5 6 7
用这个样本的频率分布估计总体分布,将频率视为概率,求等级系数X2的数学期望.
![]() 在(I)、(II)的条件下,若以“性价比”为判断标准,则哪个工厂的产品更具可购买性?说明理由.
在(I)、(II)的条件下,若以“性价比”为判断标准,则哪个工厂的产品更具可购买性?说明理由.
注:(1)产品的“性价比”=![]() ;
;
(2)“性价比”大的产品更具可购买性.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,正方体ABCD-A1B1C1D1的棱长为1,线段B1D1上有两个动点E、F且EF=![]() ,则下列结论中错误的是( )
,则下列结论中错误的是( )

A.AC⊥BEB.EF![]() 平面ABCD
平面ABCD
C.三棱锥A-BEF的体积为定值D.异面直线AE,BF所成的角为定值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知 n 个四元集合 A1 , A2 ,…, An ,每两个有且只有一个公共元 ,并且有Card(A1 ∪ A2 ∪ …∪ An)=n .试求 n 的最大值.这里 Card A 为集合A中元素的个数 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的个数为( )
①命题“![]() 中,若
中,若![]() ,则
,则![]() ”的逆命题是真命题
”的逆命题是真命题
②若命题![]() ,则
,则![]()
③“命题![]() 为真命题”是“命题
为真命题”是“命题![]() 为假命题”的充要条件
为假命题”的充要条件
④设![]() 均为非零向量,则“
均为非零向量,则“![]() ”是“
”是“![]() 与
与![]() 的夹角为锐角”的必要不充分条件
的夹角为锐角”的必要不充分条件
A.1B.2C.3D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com