练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    若n∈N*，n < 100，且二项式的展开式中存在常数项，则所有满足条件的n值的和是________．

    950

    解析试题分析：二项式的展开式Tr + 1 =,令3n–5r = 0，得,再令r = 3k，k∈N*，∴n =" 5k" < 100,∴1≤k≤19，k∈N*
    ∴所有满足条件的n值的和是5 + 10 + 15 + … + 95 =× 19 = 950．
    考点：本题考查了二项式展开式的运用
    点评：熟练运用二项式的展开式公式是解决此类问题的关键，属基础题

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    我们常用构造等式对同一个量算两次的方法来证明组合恒等式，如由等式可得，左边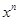的系数为，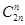
    而右边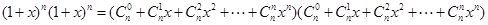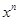， 的系数为，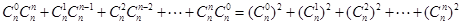
    由恒成立，可得．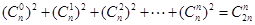
    利用上述方法，化简      ．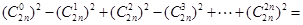

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

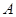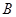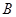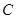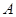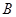    已知从地到地有2条公路可走，从地到地有3条小路可走，又从地不过地到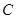地有1条水路可走，那么从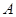地到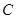地的不同走法一共有______________种．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    若等式对一切都成立，其中，，，…，为实常数，则＝           .

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    的二项展开式中的常数项为          ．（用数字作答）

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    将6位志愿者分成4组，其中两个组各2人，另两个组各1人，分赴世博会的四个不同场馆服务，不同的分配方案有       种（用数字作答）。

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    某公司计划在环海海渤经济区的大连、营口、盘锦、锦州、葫芦岛五个候选城市中投资3个不同的项目,且在同一个城市投资的项目不超过2个,则该公司不同的投资方案种数是                    (用数字作答)．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    古代“五行”学说认为：“物质分金、木、土、水、火五种属性，金克木，木克土，土克水，水克火，火克金.”将五种不同属性的物质任意排成一列，则排列中属性相克的两种物质不相邻的排列种数是                （用数字作答）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    的展开式中项的系数是        .

    查看答案和解析>>

    同步练习册答案