
我们常用构造等式对同一个量算两次的方法来证明组合恒等式,如由等式 可得,左边
可得,左边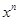 的系数为
的系数为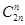 ,
,
而右边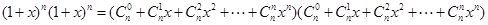 ,
, 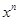 的系数为
的系数为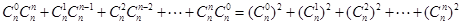 ,
,
由 恒成立,可得
恒成立,可得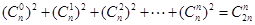 .
.
利用上述方法,化简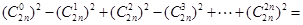 .
.

解析试题分析:构造等式(x-1)2n•(x+1)2n=(x2-1)2n,由左式可得x2n的系数为C2n2n•(-1)2nC2n0+C2n2n-1•(-1)2n-1C2n1+C2n2n-2•(-1)2n-2C2n2+…+C2n0•(-1)0C2n2n,即(C2n0)2-(C2n1)2+(C2n2)2-(C2n3)2+…+(C2n2n)2,由右式可得得x2n的系数为(-1)nC2nn,故有(C2n0)2-(C2n1)2+(C2n2)2-(C2n3)2+…+(C2n2n)2=(-1)nC2nn,
考点:本题考查了组合数的运用
点评:对于此类组合数的应用问题,常常涉及二项式定理的应用,关键要根据题意,充分利用组合数的性质.


科目:高中数学 来源: 题型:填空题
将7×7的棋盘中的2个方格染成黄色,其余的染成绿色。若一种染色法经过在棋盘的平面中旋转而得到,那么这两种染色法看着是同一种,则有 种不同的染色法.
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
关于二项式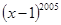 有下列命题:
有下列命题:
①该二项展开式中非常数项的系数和是1:
②该二项展开式中第六项为C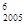
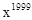 ;
;
③该二项展开式中系数最大的项是第1002项:
④当x=2006时,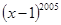 除以2006的余数是2005.
除以2006的余数是2005.
其中正确命题的序号是__________ .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com