
【题目】已知函数![]() .
.
(1)a=1时,求函数f(x)的极值;
(2)若![]() ,求f(x)的最小值g(a)的取值范围.
,求f(x)的最小值g(a)的取值范围.
【答案】(1)f(x)极小值e﹣1,无极大值;(2)[ln2﹣1,e﹣1].
【解析】
(1)代入![]() 求导可得
求导可得![]() ,再求导分析单调性与最值可知
,再求导分析单调性与最值可知![]() ,进而求得
,进而求得![]() 的极值点与单调区间以及极值.
的极值点与单调区间以及极值.
(2)求导后构造导函数![]() 得出
得出![]() ,再根据(1)中的结论可知
,再根据(1)中的结论可知![]() 恒成立,进而可得
恒成立,进而可得![]() 在定义域上单调递增.再根据零点存在定理可知
在定义域上单调递增.再根据零点存在定理可知![]() 在
在![]() 上有唯一解
上有唯一解![]() ,且
,且![]() ,进而求得最小值
,进而求得最小值![]() ,再根据隐零点问题消去参数
,再根据隐零点问题消去参数![]() ,再构造函数关于极值点
,再构造函数关于极值点![]() 的函数分析即可.
的函数分析即可.
(1)当a=1时,![]() ,则
,则![]() ,
,
令h(x)=ex﹣x,当x∈(0,+∞)时,h′(x)=ex﹣1>0,
∴在(0,+∞)上,h(x)>h(0)=1,即ex>x,
令f′(x)=0,则x=1,经检验,在(0,1)上,f′(x)<0,f(x)单调递减,在(1,+∞)上,f′(x)>0,f(x)单调递增,
∴当x=1时,函数y=f(x)取得极小值e﹣1,无极大值;
(2)![]() ,令
,令![]() ,
,
则![]() ,
,
由(1)知,当x∈(0,+∞)时,
ex>x,ex(x2﹣2x+2)﹣x>x(x2﹣2x+2)﹣x=x(x﹣1)2≥0,
∴p′(x)>0在(0,+∞)上恒成立,
∴f′(x)在定义域上单调递增,
∵![]() ,
,
∴![]() ,
,
∴方程f′(x)=0在(0,+∞)上有唯一解,
设方程f′(x)=0的解为x0,则在(0,x0)上f′(x)<0,在(x0,+∞)上f′(x)>0,且1≤x0≤2,
∴f(x)的最小值为![]() ,
,
由f′(x)=0得,![]() 代入g(a)得,
代入g(a)得,![]() ,
,
令![]() ,则
,则![]() ,
,
∵﹣x2+2x﹣2=﹣(x﹣1)2﹣1≤﹣1,
∴ex(﹣x2+2x﹣2)+x≤x﹣ex<0,
∴φ(x)在[1,2]上为减函数,
∴![]() ,
,
∴g(a)∈[ln2﹣1,e﹣1].


科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,以原点
中,以原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系. 已知曲线的极坐标方程为
轴的正半轴为极轴建立极坐标系. 已知曲线的极坐标方程为![]() ,直线 的参数方程为
,直线 的参数方程为 (
(![]() 为参数).
为参数).
(I)分别求曲线![]() 的直角坐标方程和直线
的直角坐标方程和直线![]() 的普通方程;
的普通方程;
(II)设曲线![]() 和直线
和直线![]() 相交于
相交于![]() 两点,求弦长
两点,求弦长![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).M是曲线
为参数).M是曲线![]() 上的动点,将线段OM绕O点顺时针旋转
上的动点,将线段OM绕O点顺时针旋转![]() 得到线段ON,设点N的轨迹为曲线
得到线段ON,设点N的轨迹为曲线![]() .以坐标原点O为极点,
.以坐标原点O为极点,![]() 轴正半轴为极轴建立极坐标系.
轴正半轴为极轴建立极坐标系.
(1)求曲线![]() 的极坐标方程;
的极坐标方程;
(2)在(1)的条件下,若射线![]() 与曲线
与曲线![]() 分别交于A, B两点(除极点外),且有定点
分别交于A, B两点(除极点外),且有定点![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,x∈(b﹣3,2b)是奇函数,
,x∈(b﹣3,2b)是奇函数,
(1)求a,b的值;
(2)若f(x)是区间(b﹣3,2b)上的减函数且f(m﹣1)+f(2m+1)>0,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某化工厂引进一条先进生产线生产某种化工产品,其生产的总成本![]() (万元)与年产量
(万元)与年产量![]() (吨)之间的函数关系式可以近似的表示为
(吨)之间的函数关系式可以近似的表示为![]() ,已知此生产线年产量最大为
,已知此生产线年产量最大为![]() 吨.
吨.
(1)求年产量为多少吨时,生产每吨产品的平均成本最低,并求最低成本;
(2)若每吨产品平均出厂价为40万元,那么当年产量为多少吨时,可以获得最大利润?最大利润是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知两圆C1:x2+y2-2x-6y-1=0和C2:x2+y2-10x-12y+45=0.
(1)求证:圆C1和圆C2相交;
(2)求圆C1和圆C2的公共弦所在直线的方程和公共弦长.
查看答案和解析>>
科目:高中数学 来源: 题型:
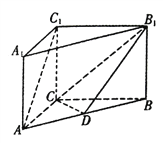
【题目】直三棱柱![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,点
,点![]() 是线段
是线段![]() 上的动点.
上的动点.
(1)当点![]() 是
是![]() 的中点时,求证:
的中点时,求证: ![]() 平面
平面![]() ;
;
(2)线段![]() 上是否存在点
上是否存在点![]() ,使得平面
,使得平面![]() 平面
平面![]() ?若存在,试求出
?若存在,试求出![]() 的长度;若不存在,请说明理由.
的长度;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com