已知(1-ax)n展开式的第r,r+1,r+2三项的二次式系数构成等差数列,第n+1-r与第n+2-r项的系数之和为0,而(1-ax)n+1展开式的第r+1与r+2项的二项式系数之比为1:2.
(1)求(1-ax)n+1展开式的中间项;
(2)求(1-ax)n的展开式中系数最大的项.
【答案】
分析:(1)利用展开式的第r,r+1,r+2三项的二项式系数构成等差数列,第n+1-r与第n+2-r项的系数之和为0,而(1-ax)
n+1展开式的第r+1与r+2项的二项式系数之比为1:2.列出方程即可求出a,n的值,然后求出中间项.
(2)利用二项式系数的性质,直接求出展开式的系数的最大项即可.
解答:解:(1-ax)
n展开式的第r,r+1,r+2三项的二项式系数构成等差数列,
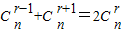
,…①;
第n+1-r与第n+2-r项的系数之和为0,
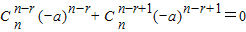
…②;
而(1-ax)
n+1展开式的第r+1与r+2项的二项式系数之比为1:2.即
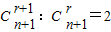
,…③;
由③得n=3r+1,…④
由①得
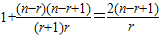
…⑤,
由④⑤解得r=2,n=7,
把r=2,n=7代入②解得a=3.
(1)(1-3x)
8展开式的中间项为
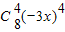
=5670x
4;
(2)求(1-3x)
7的展开式中系数最大的项在奇数项中,分别是第一项
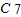
=1;第三项
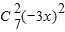
=189x
2,
第五项
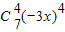
=35×3
4x
4=2835x
4,第七项
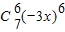
=63×3
4x
6=5103x
6.
(1-ax)
n的展开式中系数最大项是第七项
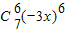
=5103x
6.
点评:本题是中档题,考查二项式定理系数的性质,考查组合数的求法,考查计算能力.

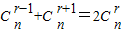 ,…①;
,…①;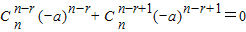 …②;
…②;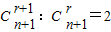 ,…③;
,…③;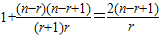 …⑤,
…⑤,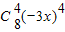 =5670x4;
=5670x4;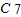 =1;第三项
=1;第三项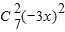 =189x2,
=189x2,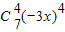 =35×34x4=2835x4,第七项
=35×34x4=2835x4,第七项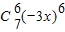 =63×34x6=5103x6.
=63×34x6=5103x6.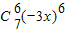 =5103x6.
=5103x6.
