
已知曲线C:![]() 过C上一点
过C上一点![]() 作一斜率为
作一斜率为![]() 的直线交曲线C于另一点
的直线交曲线C于另一点![]() ,点列
,点列![]() (
(![]() =1,2,3,???)的横坐标构成数列
=1,2,3,???)的横坐标构成数列![]() ,其中
,其中![]() .
.
(1)求![]() 与
与![]() 的关系式;
的关系式;
(2)求证:![]() 是等比数列;
是等比数列;
(3)求证:![]() .
.
 小夫子全能检测系列答案
小夫子全能检测系列答案科目:高中数学 来源: 题型:
| lim | n→∞ |
查看答案和解析>>
科目:高中数学 来源:2004全国各省市高考模拟试题汇编(天利38套)·数学 题型:044
已知曲线C的方程为:kx2+(4-k)y2=k+1(k∈R)
(Ⅰ)若曲线C是椭圆,求k的取值范围;
(Ⅱ)若曲线C是双曲线,且有一条渐近线的倾斜角是 ,求此双曲线的方程;
,求此双曲线的方程;
(Ⅲ)(理)满足(Ⅱ)的双曲线上是否存在两点P,Q关于直线l:y=x-1对称,若存在,求出过P,Q的直线方程;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源:2011年广东省广州市仲元中学高三数学专题训练:圆锥曲线方程(解析版) 题型:解答题
查看答案和解析>>
科目:高中数学 来源:高考数学一轮复习必备(第100-102课时):第十三章 导数-导数的应用(3)(解析版) 题型:解答题
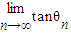 之值.
之值.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com