
设A,B,C,D是空间不共面的四个点,且满足 ·
· =0,
=0, ·
· =0,
=0, ·
· =0,则△BCD的形状是( )
=0,则△BCD的形状是( )
| A.钝角三角形 | B.直角三角形 |
| C.锐角三角形 | D.无法确定 |
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:单选题
给出下列命题: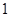 向量
向量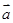 ,
, 满足
满足 ,则
,则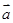 ,
, 的夹角为
的夹角为 ;
;
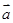


 是〈
是〈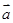 ,
, 〉为锐角的充要条件;
〉为锐角的充要条件; 将函数
将函数 的图象按向量
的图象按向量 平移,
平移,
得到函数 的图象;
的图象; 若
若

 ,则
,则 为等腰三角形。
为等腰三角形。
以上命题正确的个数是 ( )
| A.1个 | B.2个 | C.3个 | D.4个 |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
在平面斜坐标系 中,
中, 轴方向水平向右,
轴方向水平向右, 方向指向左上方,且
方向指向左上方,且 ,平面上任一点
,平面上任一点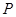 关于斜坐标系的斜坐标是这样定义的:若
关于斜坐标系的斜坐标是这样定义的:若 (其中向量
(其中向量 分别是与
分别是与 轴、
轴、 轴同方向的单位向量),则
轴同方向的单位向量),则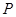 点斜坐标为
点斜坐标为 ,那么以
,那么以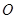 为顶点,
为顶点, 为焦点,
为焦点, 轴为对称轴的抛物线方程为
轴为对称轴的抛物线方程为
A. | B. | C. | D. |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
设e1,e2,e3,e4是某平面内的四个单位向量,其中e1⊥e2,e3与e4的夹角为45°,对这个平面内的任意一个向量a=xe1+ye2,规定经过一次“斜二测变换”得到向量a1=xe3+ e4.设向量t1=-3e3-2e4是经过一次“斜二测变换”得到的向量,则|t|是( )
e4.设向量t1=-3e3-2e4是经过一次“斜二测变换”得到的向量,则|t|是( )
| A.5 | B.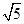 | C.73 | D. |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
设向量a=(1,-3),b=(-2,4),若表示向量4a,3b-2a,c的有向线段首尾相接能构成三角形,则向量c为( )
| A.(1,-1) | B.(-1,1) | C.(-4,6) | D.(4,-6) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com