
分析 (1)代入a值,解二次不等式即可;
(2)根据二次函数的性质直接求解即可.
解答 解:(1)当a=2时,f(x)=ax2-x+a,
由f(x)>3得2x2-x+2>3 …(2分)
解得$x<-\frac{1}{2}$或x>1…(4分)
故不等式的解集为 (-∞,$-\frac{1}{2}$∪(1,+∞)(5分)
(2)二次函数有最大值,必须a<0…(6分)
由$\frac{{4{a^2}-1}}{4a}=-2$得4a2+8a-1=0,
解得$a=-1±\frac{{\sqrt{5}}}{2}$…(9分)
由于a<0,故实数$a=-1-\frac{{\sqrt{5}}}{2}$…(10分)
点评 考查了二次不等式和二次函数的基本性质,属于基础题型,应熟练掌握.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
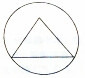 棱长为a的正四面体的四个顶点都在同一个球面上,若过该球球心的一个截面如图所示,并且图中三角形(正四面体的截面)的面积是3$\sqrt{2}$,则a等于( )
棱长为a的正四面体的四个顶点都在同一个球面上,若过该球球心的一个截面如图所示,并且图中三角形(正四面体的截面)的面积是3$\sqrt{2}$,则a等于( )| A. | 2$\sqrt{2}$ | B. | $\sqrt{2}$ | C. | 2$\sqrt{3}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | g(x)在(0,$\frac{π}{4}$)上单调递增,且为奇函数 | |
| B. | g(x)的最大值为1,其图象关于直线x=$\frac{π}{2}$对称 | |
| C. | g(x)在(-$\frac{3π}{8}$,$\frac{π}{8}$)上单调递增,且为偶函数 | |
| D. | g(x)的周期为π,其图象关于点($\frac{3π}{8}$,0)对称 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{\sqrt{2}}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com