
【题目】如图,已知抛物线x2=2py(p>0)的焦点为F(0,1),过F的两条动直线AB,CD与抛物线交出A、B、C、D四点,直线AB,CD的斜率存在且分别是k1(k1>0),k2.
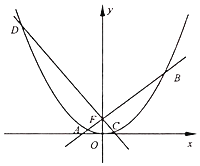
(Ⅰ)若直线BD过点(0,3),求直线AC与y轴的交点坐标
(Ⅱ)若k1﹣k2=2,求四边形ACBD面积的最小值.
【答案】(Ⅰ)(0,![]() );(Ⅱ)32.
);(Ⅱ)32.
【解析】
(Ⅰ)抛物线方程为![]() ,设
,设![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,直线
,直线![]() 代入抛物线方程,当
代入抛物线方程,当![]() 时,得
时,得![]() ,
,![]() ,当
,当![]() 时,得
时,得![]() ,进而可得
,进而可得![]() 值为
值为![]() ,写出直线AC方程,令
,写出直线AC方程,令![]() 得
得![]() ,进而得出结论;
,进而得出结论;
(Ⅱ)设![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,直线l的方程是
,直线l的方程是![]() ,联立抛物线方程,由韦达定理可得,
,联立抛物线方程,由韦达定理可得,![]() ,再求出点C到AB的距离d1,点D到AB的距离d2,
,再求出点C到AB的距离d1,点D到AB的距离d2,![]() ,化简得
,化简得![]() ,设
,设![]() ,求导,分析单调性,进而得出
,求导,分析单调性,进而得出![]() .
.
(Ⅰ)由题意可得抛物线方程为![]() ,
,
设直线![]() 代入抛物线方程得
代入抛物线方程得![]() ,
,
设![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
当![]() 时,得
时,得![]() ,
,![]() ,
,
当![]() 时,
时,![]() ,
,
所以![]() ,
,
直线AC方程是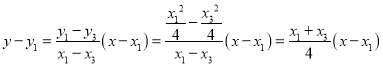 ,
,
令![]() 得
得![]() ,
,
故直线AC与y轴交点坐标是![]() ;
;
(Ⅱ)设直线l的方程是![]() ,代入
,代入![]() 得
得![]() ,
,
设![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
则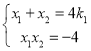 ,
,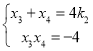 ,
,
![]() ,
,
点C到AB的距离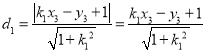 ,
,
点D到AB的距离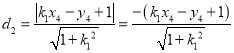 ,
,
则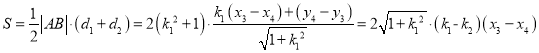
![]() ,
,
设![]() ,
,
则![]() ,
,
所以![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
所以在![]() 内
内![]() 最小值
最小值![]() ,
,
故当![]() ,
,![]() 时,
时,![]() .
.


科目:高中数学 来源: 题型:
【题目】如图, ![]() 为圆
为圆![]() 的直径,点
的直径,点![]() ,
, ![]() 在圆
在圆![]() 上,
上, ![]() ,矩形
,矩形![]() 和圆
和圆![]() 所在的平面互相垂直,已知
所在的平面互相垂直,已知![]() ,
, ![]() .
.
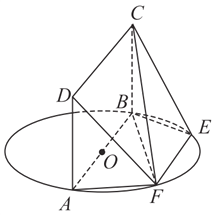
(Ⅰ)求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)求直线![]() 与平面
与平面![]() 所成角的大小;
所成角的大小;
(Ⅲ)当![]() 的长为何值时,二面角
的长为何值时,二面角![]() 的大小为
的大小为![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
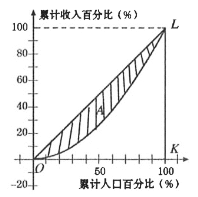
【题目】为了研究国民收入在国民之间的分配,避免贫富过分悬殊,美国统计学家劳伦茨提出了著名的劳伦茨曲线,如图所示:劳伦茨曲线为直线![]() 时,表示收入完全平等,劳伦茨曲线为折线
时,表示收入完全平等,劳伦茨曲线为折线![]() 时,表示收入完全不平等记区域
时,表示收入完全不平等记区域![]() 为不平等区域,
为不平等区域,![]() 表示其面积,
表示其面积,![]() 为
为![]() 的面积.将
的面积.将![]() ,称为基尼系数.对于下列说法:
,称为基尼系数.对于下列说法:
①![]() 越小,则国民分配越公平;
越小,则国民分配越公平;
②设劳伦茨曲线对应的函数为![]() ,则对
,则对![]() ,均有
,均有![]() ;
;
③若某国家某年的劳伦茨曲线近似为![]() ,则
,则![]() ;
;
④若某国家某年的劳伦茨曲线近似为![]() ,则
,则![]() .
.
其中不正确的是:( )
A.①④B.②③C.①③④D.①②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左焦点在抛物线
的左焦点在抛物线![]() 的准线上,且椭圆的短轴长为2,
的准线上,且椭圆的短轴长为2,![]() 分别为椭圆的左,右焦点,
分别为椭圆的左,右焦点,![]() 分别为椭圆的左,右顶点,设点
分别为椭圆的左,右顶点,设点![]() 在第一象限,且
在第一象限,且![]() 轴,连接
轴,连接![]() 交椭圆于点
交椭圆于点![]() ,直线
,直线![]() 的斜率为
的斜率为![]() .
.
(Ⅰ)求椭圆的方程;
(Ⅱ)若三角形![]() 的面积等于四边形
的面积等于四边形![]() 的面积,求
的面积,求![]() 的值;
的值;
(Ⅲ)设点![]() 为
为![]() 的中点,射线
的中点,射线![]() (
(![]() 为原点)与椭圆交于点
为原点)与椭圆交于点![]() ,满足
,满足![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某省开展“精准脱贫,携手同行”的主题活动,某贫困县统计了100名基层干部走访贫困户的数量,并将走访数量分成5组,统计结果见下表.
走访数量区间 | 频数 | 频率 |
| b | |
| 10 | |
| 38 | |
| a | 0.27 |
| 9 | |
总计 | 100 | 1.00 |
(1)求a与b的值;
(2)根据表中数据,估计这100名基层干部走访数量的中位数(精确到个位);
(3)如果把走访贫困户不少于35户视为“工作出色”,按照分层抽样,从“工作出色”的基层干部中抽取4人,再从这4人中随机抽取2人,求其中有1人走访贫困户不少于45户的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() .
.
(1)求函数![]() 的单调递减区间;
的单调递减区间;
(2)若![]() ,对于给定实数
,对于给定实数![]() ,总存在实数
,总存在实数![]() ,使得关于
,使得关于![]() 的方程
的方程![]() 恰有3个不同的实数根.
恰有3个不同的实数根.
(i)求实数![]() 的取值范围;
的取值范围;
(ii)记![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某快餐连锁店招聘外卖骑手,该快餐连锁店提供了两种日工资方案:方案(a)规定每日底薪50元,快递业务每完成一单提成3元;方案(b)规定每日底薪100元,快递业务的前44单没有提成,从第45单开始,每完成一单提成5元,该快餐连锁店记录了每天骑手的人均业务量,现随机抽取100天的数据,将样本数据分为[ 25,35),[35,45),[45,55),[55,65),[65,75),[75,85),[85,95]七组,整理得到如图所示的频率分布直方图.

(1)随机选取一天,估计这一天该连锁店的骑手的人均日快递业务量不少于65单的概率;
(2)从以往统计数据看,新聘骑手选择日工资方案(a)的概率为![]() ,选择方案(b)的概率为
,选择方案(b)的概率为![]() .若甲、乙、丙三名骑手分别到该快餐连锁店应聘,三人选择日工资方案相互独立,求至少有两名骑手选择方案(a)的概率;
.若甲、乙、丙三名骑手分别到该快餐连锁店应聘,三人选择日工资方案相互独立,求至少有两名骑手选择方案(a)的概率;
(3)若仅从人均日收入的角度考虑,请你利用所学的统计学知识为新聘骑手做出日工资方案的选择,并说明理由.(同组中的每个数据用该组区间的中点值代替)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,上顶点为A,过
,上顶点为A,过![]() 的直线
的直线![]() 与y轴交于点M,满足
与y轴交于点M,满足![]() (O为坐标原点),且直线l与直线
(O为坐标原点),且直线l与直线![]() 之间的距离为
之间的距离为![]() .
.
(1)求椭圆C的方程;
(2)在直线![]() 上是否存在点P,满足
上是否存在点P,满足![]() ?存在,指出有几个这样的点(不必求出点的坐标);若不存在,请说明理由.
?存在,指出有几个这样的点(不必求出点的坐标);若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com