
【题目】设函数![]() .
.
(1)求函数![]() 的单调递减区间;
的单调递减区间;
(2)若![]() ,对于给定实数
,对于给定实数![]() ,总存在实数
,总存在实数![]() ,使得关于
,使得关于![]() 的方程
的方程![]() 恰有3个不同的实数根.
恰有3个不同的实数根.
(i)求实数![]() 的取值范围;
的取值范围;
(ii)记![]() ,求证:
,求证:![]() .
.
【答案】(1)单调递减区间是![]() ,
,![]() ;(2)(i)
;(2)(i)![]() ;(ii)证明见详解.
;(ii)证明见详解.
【解析】
(1)当![]() ,
,![]() ,当
,当![]() 时,可知
时,可知![]() ,此时
,此时![]() 无单调递减区间;当
无单调递减区间;当![]() 时,令
时,令![]() ,可得
,可得![]() ,再根据
,再根据![]() 为偶函数,即可求出函数
为偶函数,即可求出函数 ![]() 的单调递减区间;
的单调递减区间;
(2)(i)![]()
![]() ,令
,令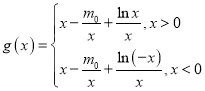 ,则
,则![]() ,令
,令![]() ,利用导数可得
,利用导数可得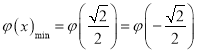 ;再分别对
;再分别对![]() 和
和![]() ,两种情况分类讨论,根据函数的单调性和奇偶性以及对称性进行分析,即可求出结果;
,两种情况分类讨论,根据函数的单调性和奇偶性以及对称性进行分析,即可求出结果;
(ii)由![]() 的四个根为
的四个根为![]() ,
,![]() ,
,![]() ,
,![]() ,不妨设
,不妨设![]() ,由于
,由于![]() 为偶函数,则
为偶函数,则![]() ,
, 化简整理可得
化简整理可得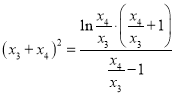 ,令
,令![]() ,
,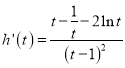 ,令
,令![]() ,根据导数在函数单调性和最值的应用,即可求证结果.
,根据导数在函数单调性和最值的应用,即可求证结果.
(1)当![]() ,
,![]() ,当
,当![]() ,
,![]() ;当
;当![]() ,
,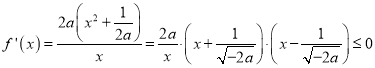 ,∴
,∴![]() .
.
又![]() 为偶函数,∴当
为偶函数,∴当![]() 时,
时,![]() 的单调递减区间是
的单调递减区间是![]() ,
,![]() ,
,
当![]() 时,
时,![]() 无单调递减区间.
无单调递减区间.
(2)(i)![]()
 ,令
,令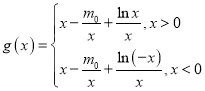 ,
,
则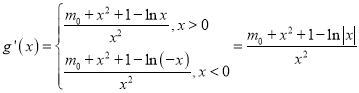 ,
,
令![]() ,
,![]() ,
,
∴![]() 在
在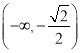 递减,
递减,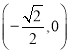 递增,
递增,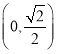 递减,
递减,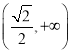 递增.
递增.
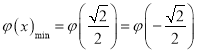 .
.
①当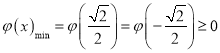 时,可得
时,可得![]() ,此时
,此时![]() ,所以
,所以![]() 在
在![]() 递减,在
递减,在![]() 递增,则
递增,则![]() 至多2个零点,不符合题意.
至多2个零点,不符合题意.
②当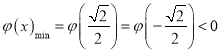 ,则
,则![]() 有4个不同实根,即
有4个不同实根,即![]() 时,
时,![]() 有2个不同实根,此时
有2个不同实根,此时![]() .
.
其中![]() ,
,![]() (极大),
(极大),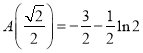 ,设
,设![]() 的4个实根为
的4个实根为![]() ,则
,则![]() 极大,
极大,![]() 极小,
极小,![]() 极大,
极大,![]() 极小,由于
极小,由于![]() 为奇函数,所以极值关于原点对称,
为奇函数,所以极值关于原点对称,![]() ,
,
![]() ,∴
,∴![]() ,当
,当![]() 时
时![]() 有3个零点.
有3个零点.
(ii)由![]() 的四个根为
的四个根为![]() ,
,![]() ,
,![]() ,
,![]() ,不妨设
,不妨设![]() ,由于
,由于![]() 为偶函数,则
为偶函数,则![]() ,
,
![]() ,
,
∴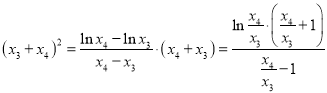 ,
,
令![]() ,
,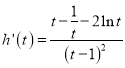 ,
,
令![]() ,
,![]() ,所以
,所以![]() 单调递增,
单调递增,
![]() ,所以
,所以![]() ,
,![]() 单调递增,则
单调递增,则![]() ,
,
所以![]() ,
,![]() .
.


 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案科目:高中数学 来源: 题型:
【题目】“一带一路”是“丝绸之路经济带”和“21世纪海上丝绸之路”的简称,旨在积极发展我国与沿线国家经济合作关系,共同打造政治互信、经济融合、文化包容的命运共同体.自2013年以来,“一带一路”建设成果显著.下图是2013-2017年,我国对“一带一路”沿线国家进出口情况统计图.下列描述错误的是( )
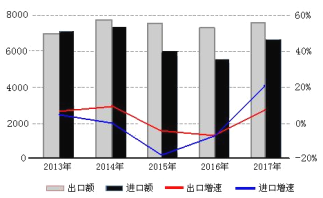
A.这五年,2013年出口额最少
B.这五年,出口总额比进口总额多
C.这五年,出口增速前四年逐年下降
D.这五年,2017年进口增速最快
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知抛物线x2=2py(p>0)的焦点为F(0,1),过F的两条动直线AB,CD与抛物线交出A、B、C、D四点,直线AB,CD的斜率存在且分别是k1(k1>0),k2.
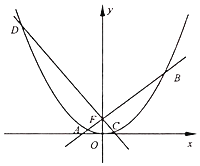
(Ⅰ)若直线BD过点(0,3),求直线AC与y轴的交点坐标
(Ⅱ)若k1﹣k2=2,求四边形ACBD面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】空气质量指数AQI是反映空气质量状况的指数,AQI指数值越小,表明空气质量越好,其对应关系如下表:
AQI指数值 | 0~50 | 51~100 | 101~150 | 151~200 | 201~300 | >300 |
空气质量 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
下图是某市10月1日—20日AQI指数变化趋势:

下列叙述错误的是
A. 这20天中AQI指数值的中位数略高于100
B. 这20天中的中度污染及以上的天数占![]()
C. 该市10月的前半个月的空气质量越来越好
D. 总体来说,该市10月上旬的空气质量比中旬的空气质量好
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某区在2019年教师招聘考试中,参加![]() 、
、![]() 、
、![]() 、
、![]() 四个岗位的应聘人数、录用人数和录用比例(精确到1%)如下:
四个岗位的应聘人数、录用人数和录用比例(精确到1%)如下:
岗位 | 男性应聘人数 | 男性录用人数 | 男性录用比例 | 女性应聘人数 | 女性录用人数 | 女性录用比例 |
| 269 | 167 | 62% | 40 | 24 | 60% |
| 217 | 69 | 32% | 386 | 121 | 31% |
| 44 | 26 | 59% | 38 | 22 | 58% |
| 3 | 2 | 67% | 3 | 2 | 67% |
总计 | 533 | 264 | 50% | 467 | 169 | 36% |
(1)从表中所有应聘人员中随机抽取1人,试估计此人被录用的概率;
(2)将应聘![]() 岗位的男性教师记为
岗位的男性教师记为![]() ,女性教师记为
,女性教师记为![]() ,现从应聘
,现从应聘![]() 岗位的6人中随机抽取2人.
岗位的6人中随机抽取2人.
(i)试用所给字母列举出所有可能的抽取结果;
(ii)设![]() 为事件“抽取的2人性别不同”,求事件
为事件“抽取的2人性别不同”,求事件![]() 发生的概率.
发生的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com