
分析 若f(2)=1,结合抽象函数将不等式化为f(x+3)-f($\frac{1}{x}$)<f(2)+f(2),再进行转化,结合函数的单调性解不等式即可.
解答 解:∵f(2)=1,∴2=1+1=f(2)+f(2),
对于不等式f(x+3)-f($\frac{1}{x}$)<2,有$\left\{\begin{array}{l}{x+3>0}\\{\frac{1}{x}>0}\end{array}\right.$,
解可得x>0,
∴不等式f(x+3)-f($\frac{1}{x}$)<2,
等价为不等式f(x+3)-f($\frac{1}{x}$)<f(2)+f(2),
∴f(x2+3x)-f(2)<f(2),
即f($\frac{{x}^{2}+3x}{2}$)<f(2),
∵f(x)是(0,+∞)上的增函数,
∴0<$\frac{{x}^{2}+3x}{2}$<2,解得-4<x<-3或0<x<1,
又由x>0,
即不等式的解集为(0,1).
点评 本题主要考查抽象函数的应用,根据函数单调性将不等式进行转化是解决本题的关键.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源:2016-2017学年湖南益阳市高二9月月考数学(文)试卷(解析版) 题型:选择题
已知等差数列{an}的前n项和为Sn,a5=5,S5=15,则数列{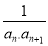 }的前100项和为
}的前100项和为
A.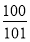 B.
B.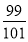 C.
C.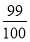 D.
D.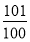
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | -1 | C. | 0 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
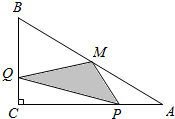 如图,△ABC中,∠C=90°,M是AB的中点,动点P从点A出发,沿AC方向匀速运动到终点C,动点Q从点C出发,沿CB方向匀速运动到终点B.已知P,Q两点同时出发,并同时到达终点,连接MP,MQ,PQ.在整个运动过程中,△MPQ的面积大小变化情况是( )
如图,△ABC中,∠C=90°,M是AB的中点,动点P从点A出发,沿AC方向匀速运动到终点C,动点Q从点C出发,沿CB方向匀速运动到终点B.已知P,Q两点同时出发,并同时到达终点,连接MP,MQ,PQ.在整个运动过程中,△MPQ的面积大小变化情况是( )| A. | 一直增大 | B. | 一直减小 | C. | 先减小后增大 | D. | 先增大后减小 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-1,2] | B. | [-1,4] | C. | [$\frac{1}{2}$,4] | D. | [$\frac{1}{2}$,2] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | 3 | D. | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com