
(1)1.9975精确到0.001的近似值为________.
(2)在(1+x+x2)(1-x)10的展开式中,x5的系数是________.
(3)1919除以5的余数为________;
(4)和S=![]() +2
+2![]() +3
+3![]() +…+10
+…+10![]() C的值为________.
C的值为________.
|
思路 本题涉及的都是二项式定理内容的应用,它们一般都有明确的解题思路,应注意总结. 解答 (1)1.9975=(2-0.003)5=25-5×24×0.003+10×23×0.0032-10×22×0.0033+…,显然|T6|<|T5|<|T4|=1.08×106, ∴1.9975≈32-0.24+0.00072≈31.761; (2)(1+x+x2)(1-x)10=(1-x3)(1-x)9=(1-x)9-x3(1-x)9,其展开式x5的系数为- (3)1919=(20-1)19=2019- =(2019- ∴1919除以5的余数为4; (4)解一:通项分析法:∵k ∴S= =10( 解二:逆向相加法,设S= ∴S=10×29=5120. 评析 用二项式定理讨论一个式子被m除的余数时,一般把其主要式子写成(a+bm)n(a、b∈Z)的形式,即首项外其余各项均能被m整除.而对于不满足 |


 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案科目:高中数学 来源: 题型:
| cos2x | ||
sin(x+
|
| 4 |
| 3 |
| 1 |
| 9 |
| 1 |
| 9 |
| 3π |
| 2 |
| 3π |
| 4 |
| 3π |
| 4 |
| ||
| 2 |
| ||
| 2 |
| a |
| b |
| c |
| a |
| b |
| c |
| 0 |
| a |
| b |
| c |
| a |
| b |
| a |
| a |
| b |
| c |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
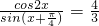 ,则sin2x的值为________.
,则sin2x的值为________.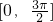 上的函数y=f(x)的图象关于直线
上的函数y=f(x)的图象关于直线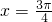 对称,当
对称,当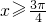 时,f(x)=cosx,如果关于x的方程f(x)=a有四个不同的解,则实数a的取值范围为________.
时,f(x)=cosx,如果关于x的方程f(x)=a有四个不同的解,则实数a的取值范围为________. 满足
满足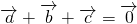 ,
,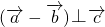 ,
, ,若
,若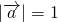 ,则
,则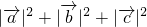 的值是________.
的值是________.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| cos2x | ||
sin(x+
|
| 4 |
| 3 |
| 3π |
| 2 |
| 3π |
| 4 |
| 3π |
| 4 |
| a |
| b |
| c |
| a |
| b |
| c |
| 0 |
| a |
| b |
| c |
| a |
| b |
| a |
| a |
| b |
| c |
查看答案和解析>>
科目:高中数学 来源:2011-2012学年北京市通州区潞河中学高一(上)期末数学试卷(解析版) 题型:解答题
 ,则sin2x的值为______.
,则sin2x的值为______. 上的函数y=f(x)的图象关于直线
上的函数y=f(x)的图象关于直线 对称,当
对称,当 时,f(x)=cosx,如果关于x的方程f(x)=a有四个不同的解,则实数a的取值范围为______
时,f(x)=cosx,如果关于x的方程f(x)=a有四个不同的解,则实数a的取值范围为______查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com