练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    直线l：y=x与园x2+y2-2x-6y=0相交A、B两点，则|AB|=
     
    ．
    考点：直线与圆的位置关系
    专题：直线与圆
    分析：利用直线与圆的位置关系，得到弦心距、半径与半弦长的关系，解直角三角形求弦长．
    解答： 解：因为直线l：y=x与园x2+y2-2x-6y=0相交A、B两点，
    并且圆心为（1，3），半径为
    		10
    ，
    所以弦心距为圆心到直线l的距离为
    |1-3|
    		2
    =
    		2
    ，
    所以
    1
    2
    AB=
    		(
    		10
    )2-(
    		2
    )2
    =2
    		2
    ，
    所以AB=4
    		2
    ；
    故答案为：4
    		2
    ．
    点评：本题考查了通过直线与圆的位置关系求弦心距、半径或者弦长，经常考查，属于基础题．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    设集合U={1，2，3，4，5}，A={1，2，3}，B={2，5}，则（∁UA）∩（∁UB）=（　　）
    A、{2}B、{2，3}
    C、{4}D、{1，3}

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    等差数列{an}前项和Sn满足S20=S40，则S60=
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    实数x、y满足不等式组
    2x-y≥0
    x+y-2≥0
    6x+3y≤18
    ，且z=ax+y（a＞0）取最小值的最优解有无穷多个，则实数a的取值是（　　）
    A、-
    4
    5
    B、1
    C、2
    D、无法确定

    查看答案和解析>>

    科目：高中数学 来源： 题型：

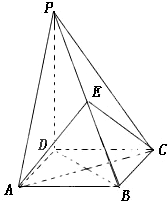    如图，四棱锥P--ABCD的底面是正方形，PD⊥底面ABCD，点E为PB的中点．且PD=
    		2
    AB
    （1）求证：平面AEC⊥平面PDB；
    （2）求AE与平面PDB所成的角的大小．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    设集合A={x|3≤x＜7}，B={x|2＜x＜7}．求：
    （1）A∪B；        
    （2）（∁RA）∩B．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如图，正三棱柱ABC-A1B1C1的侧棱长和底面边长均为2，D是BC的中点．
    （Ⅰ）求证：AD⊥平面B1BCC1；
    （Ⅱ）求证：A1B∥平面ADC1．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知椭圆
    x2
    a2
    +
    y2
    b2
    =1（a＞b＞0）的两个焦点分别为F1、F2．若椭圆上存在点P，使得|
    PF1
    +
    PF2
    |=|
    F1F2
    |成立，则
    b
    a
    的取值范围为
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    下列说法中正确的是（　　）
    A、频率是概率的近似值，随着试验次数增加，频率会越来越接近概率
    B、要从1002名学生中用系统抽样的方法选取一个容量为20的样本，需要剔除2名学生，这样对被剔除者不公平
    C、用秦九韶算法计算多项式f（x）=12+35x+9x3+5x5+3x6在当x=-1时的值时要用到6次加法和15次乘法
    D、数据2，3，4，5的方差是数据4，6，8，10的方差的一半

    查看答案和解析>>

    同步练习册答案