
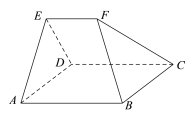
【题目】如图,在五面体![]() 中,四边形
中,四边形![]() 是边长为
是边长为![]() 的正方形,平面
的正方形,平面![]() ⊥平面
⊥平面![]() ,
, ![]() .
.
(Ⅰ) 求证:![]() ;
;
(Ⅱ) 求证:平面![]() ⊥平面
⊥平面![]() ;
;
(Ⅲ) 在线段![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() ⊥平面
⊥平面![]() ? 说明理由.
? 说明理由.
【答案】(Ⅰ)详见解析(Ⅱ)详见解析(Ⅲ)存在点N符合题意
【解析】
(Ⅰ) 推导出AB∥CD.由此能证明CD∥平面ABFE.(Ⅱ) 推导出AE⊥DE,AB⊥AD,从而AB⊥平面ADE,进而 AB⊥DE,由此能证明DE⊥平面ABFE,从而平面ABFE⊥平面CDEF.(Ⅲ)取CD的中点N,连接FN,推导出四边形EDNF是平行四边形,从而FN∥DE,由DE⊥平面ABFE,能证明FN⊥平面ABFE.
证明:(Ⅰ)在五面体![]() 中,因为四边形
中,因为四边形![]() 是正方形,
是正方形,
所以![]() .
.
因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
(Ⅱ)因为![]() ,
,![]() ,
,
所以![]() ,所以
,所以![]() ,即
,即![]() .
.
因为四边形![]() 是正方形,所以
是正方形,所以![]() .
.
因为平面![]() ⊥平面
⊥平面![]() ,平面
,平面![]()
![]() 平面
平面![]() ,
,
![]()
所以![]() ⊥平面
⊥平面![]() .
.
因为![]() ,所以
,所以![]() ⊥
⊥![]() .
.
因为![]() 所以
所以![]() ⊥平面
⊥平面![]()
因为![]() ,所以平面
,所以平面![]() ⊥平面
⊥平面![]() .
.
(Ⅲ)在线段![]() 上存在点
上存在点![]() ,使得
,使得![]() ⊥平面
⊥平面![]() .
.
证明如下:
取![]() 的中点
的中点![]() ,连接
,连接![]() .
.

由(Ⅰ)知,![]() ,
,
![]() ,
,
所以![]() .
.
因为![]()
所以![]() .
.
所以四边形![]() 是平行四边形.
是平行四边形.
所以![]() .
.
由(Ⅱ)知,![]() ⊥平面
⊥平面![]() ,
,
所以![]() .
.


科目:高中数学 来源: 题型:
【题目】从某工厂生产的某种产品中抽取1000件,测量这些产品的一项质量指标值,由测量结果得如下频率分布直方图:
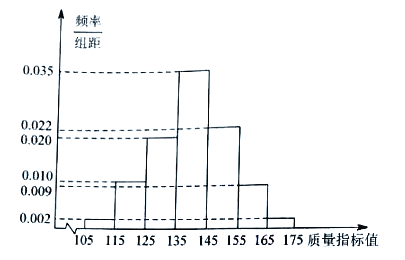
(1)求这1000件产品质量指标值的样本平均数![]() 和样本方差
和样本方差![]() (同一组数据用该区间的中点值作代表)
(同一组数据用该区间的中点值作代表)
(2)由频率分布直方图可以认为,这种产品的质量指标值![]() 服从正态分布
服从正态分布![]() ,其中以
,其中以![]() 近似为样本平均数
近似为样本平均数![]() ,
,![]() 近似为样本方差
近似为样本方差![]() .
.
(ⅰ)利用该正态分布,求![]() ;
;
(ⅱ)某用户从该工厂购买了100件这种产品,记![]() 表示这100件产品中质量指标值为于区间(127.6,140)的产品件数,利用(ⅰ)的结果,求
表示这100件产品中质量指标值为于区间(127.6,140)的产品件数,利用(ⅰ)的结果,求![]() .
.
附:![]() .若
.若![]() ,则
,则![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】第35届牡丹花会期间,我班有5名学生参加志愿者服务,服务场所是王城公园和牡丹公园.
(1)若学生甲和乙必须在同一个公园,且甲和丙不能在同一个公园,则共有多少种不同的分配方案?
(2)每名学生都被随机分配到其中的一个公园,设![]() 分别表示5名学生分配到王城公园和牡丹公园的人数,记
分别表示5名学生分配到王城公园和牡丹公园的人数,记![]() ,求随机变量
,求随机变量![]() 的分布列和数学期望
的分布列和数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 过点
过点 ![]() ,且离心率为
,且离心率为![]() .设
.设![]() 为椭圆
为椭圆![]() 的左、右顶点,P为椭圆上异于
的左、右顶点,P为椭圆上异于![]() 的一点,直线
的一点,直线![]() 分别与直线
分别与直线![]() 相交于
相交于![]() 两点,且直线
两点,且直线![]() 与椭圆
与椭圆![]() 交于另一点
交于另一点![]() .
.
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)求证:直线![]() 与
与![]() 的斜率之积为定值;
的斜率之积为定值;
(Ⅲ)判断三点![]() 是否共线,并证明你的结论.
是否共线,并证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)是定义在R上的奇函数,当x>0时,![]() .
.
(1)求f(x)的解析式;
(2)设x∈[1,2]时,函数![]() ,是否存在实数m使得g(x)的最小值为6,若存在,求m的取值;若不存在,说明理由.
,是否存在实数m使得g(x)的最小值为6,若存在,求m的取值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为考察某动物疫苗预防某种疾病的效果,现对200只动物进行调研,并得到如下数据:
未发病 | 发病 | 合计 | |
未注射疫苗 | 20 | 60 | 80 |
注射疫苗 | 80 | 40 | 120 |
合计 | 100 | 100 | 200 |
(附: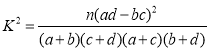 )
)
| 0.05 | 0.01 | 0.005 | 0.001 |
| 3.841 | 6.635 | 7.879 | 10.828 |
则下列说法正确的:( )
A.至少有99.9%的把握认为“发病与没接种疫苗有关”
B.至多有99%的把握认为“发病与没接种疫苗有关”
C.至多有99.9%的把握认为“发病与没接种疫苗有关”
D.“发病与没接种疫苗有关”的错误率至少有0.01%
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com