练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

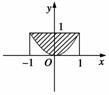
    利用计算机随机模拟方法计算图中阴影部分(如图所示)．第一步：利用计算机产生两个0～1之间的均匀随机数，x，y，其中－1＜x＜1,0＜y＜1；

    第二步：拟(x，y)为点的坐标．共做此试验N次．若落在阴影部分的点的个数为N1，

    则可以计算阴影部分的面积S.

    例如，做了2 000次试验，即N＝2 000，

    模拟得到N1＝1 396，

    所以S＝________.


    1.396

    [解析]　根据题意：点落在阴影部分的概率是，

    矩形的面积为2，阴影部分的面积为S，

    则有＝，所以S＝1.396.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    某人进行打靶练习，共射击10次，其中有2次10环，3次9环，4次8环，1次脱靶，在这次练习中，这个人中靶的频率是________，中9环的概率是________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    用计算机随机模拟掷骰子的试验，估计出现2点的概率，下列步骤中不正确的是  (　　)

    A．用计算器的随机函数RANDI(1,7)或计算机的随机函数RANDBETWEEN(1,7)产生6个不同的1到6之间的取整数值的随机数x，如果x＝2，我们认为出现2点

    B．我们通常用计数器n记录做了多少次掷骰子试验，用计数器m记录其中有多少次出现2点，置n＝0，m＝0

    C．出现2点，则m的值加1，即m＝m＋1；否则m的值保持不变

    D．程序结束．出现2点的频率作为概率的近似值

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    利用计算机产生0～1之间的均匀随机数a，则事件“3a－1＜0”发生的概率为________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    用均匀随机数进行随机模拟，可以解决(　　)

    A．只能求几何概型的概率，不能解决其他问题

    B．不仅能求几何概型的概率，还能计算图形的面积

    C．不但能估计几何概型的概率，还能估计图形的面积

    D．最适合估计古典概型的概率

    查看答案和解析>>

    科目：高中数学 来源： 题型：


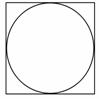
    在如图的正方形中随机撒一把芝麻，用随机模拟的方法来估计圆周率π的值．如果撒了1 000粒芝麻，落在圆内的芝麻总数是776粒，求这次模拟中π的估计值．(精确到0.001)

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知函数：①y＝2x；②y＝log2x；③y＝x－1；④y＝x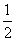；则下列函数图象(第一象限部分)从左到右依次与函数序号的对应顺序是(　　)

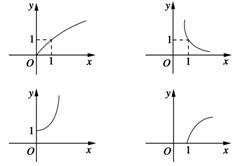
    A．②①③④                          B．②③①④

    C．④①③②                          D．④③①②

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    下列四个图像中，表示的不是函数图像的是(　　)

     

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    某城市有甲，乙两家乒乓球俱乐部，两家设备和服务都很好，但收费方式不同．甲家每张球台每小时5元；乙家按月计费，一个月中30小时以内(含30小时)每张球台90元，超过30小时的部分每张球台每小时2元．小张准备下个月从这两家中的一家租一张球台开展活动，其活动时间不少于15小时，但不超过40小时．设在甲家租一张球台开展活动x小时的收费为f(x)元(15≤x≤40)，在乙家租一张球台开展活动x小时的收费为g(x)元(15≤x≤40)．

    (1)求f(x)和g(x)；

    (2)问：小张选择哪家比较合算？为什么？

    查看答案和解析>>

    同步练习册答案