
某城市有甲,乙两家乒乓球俱乐部,两家设备和服务都很好,但收费方式不同.甲家每张球台每小时5元;乙家按月计费,一个月中30小时以内(含30小时)每张球台90元,超过30小时的部分每张球台每小时2元.小张准备下个月从这两家中的一家租一张球台开展活动,其活动时间不少于15小时,但不超过40小时.设在甲家租一张球台开展活动x小时的收费为f(x)元(15≤x≤40),在乙家租一张球台开展活动x小时的收费为g(x)元(15≤x≤40).
(1)求f(x)和g(x);
(2)问:小张选择哪家比较合算?为什么?
[解析] (1)f(x)=5x(15≤x≤40);
g(x)=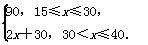
(2)由f(x)=g(x),得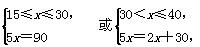
即x=18或x=10(舍).
当15≤x<18时,f(x)-g(x)=5x-90<0,
即f(x)<g(x),应选甲家;
当x=18时,f(x)=g(x),即可以选甲家也可以选乙家.
当18<x≤30时,f(x)-g(x)=5x-90>0,
即f(x)>g(x),应选乙家.
当30<x≤40时,
f(x)-g(x)=5x-(2x+30)=3x-30>0,
即f(x)>g(x),应选乙家.
综上所述:当15≤x<18时,选甲家;
当x=18时,可以选甲家也可以选乙家;
当18<x≤40时,选乙家.


科目:高中数学 来源: 题型:
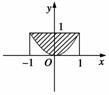
利用计算机随机模拟方法计算图中阴影部分(如图所示).第一步:利用计算机产生两个0~1之间的均匀随机数,x,y,其中-1<x<1,0<y<1;
第二步:拟(x,y)为点的坐标.共做此试验N次.若落在阴影部分的点的个数为N1,
则可以计算阴影部分的面积S.
例如,做了2 000次试验,即N=2 000,
模拟得到N1=1 396,
所以S=________.
查看答案和解析>>
科目:高中数学 来源: 题型:
设a,b,k是实数,二次函数f(x)=x2+ax+b满足:f(k-1)与f(k)异号,f(k+1)与f(k)异号.在以下关于f(x)的零点的说法中,正确的是( )
A.该二次函数的零点都小于k
B.该二次函数的零点都大于k
C.该二次函数的两个零点之间差一定大于2
D.该二次函数的零点均在区间(k-1,k+1)内
查看答案和解析>>
科目:高中数学 来源: 题型:
已知y=x(x-1)(x+1)的图象如图所示.令f(x)=x(x-1)(x+1)+0.01,则下列关于f(x)=0的解叙述正确的是________.
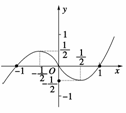
①有三个实根;
②x>1时恰有一实根;
③当0<x<1时恰有一实根;
④当-1<x<0时恰有一实根;
⑤当x<-1时恰有一实根(有且仅有一实根).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com