设a.b.k是实数.二次函数f(x)＝x2+ax+b满足:f(k-1)与f(k)异号.f(k+1)与f(k)异号．在以下关于f(x)的零点的说法中.正确的是( ) A．该二次函数的零点都小于k B．该二次函数的零点都大于k C．该二次函数的两个零点之间差一定大于2 D．该二次函数的零点均在区间(k-1.k+1)内题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

设a，b，k是实数，二次函数f(x)＝x²＋ax＋b满足：f(k－1)与f(k)异号，f(k＋1)与f(k)异号．在以下关于f(x)的零点的说法中，正确的是(　　)

A．该二次函数的零点都小于k

B．该二次函数的零点都大于k

C．该二次函数的两个零点之间差一定大于2

D．该二次函数的零点均在区间(k－1，k＋1)内

[解析]　由题意得f(k－1)·f(k)＜0，f(k)·f(k＋1)＜0，由零点的存在性定理可知，在区间(k－1，k)，(k，k＋1)内各有一个零点，零点可能是区间内的任何一个值，故D正确．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

利用计算机产生0～1之间的均匀随机数a，则事件“3a－1＜0”发生的概率为________．

查看答案和解析>>

科目：高中数学 来源： 题型：

下列四个图像中，表示的不是函数图像的是(　　)

查看答案和解析>>

科目：高中数学 来源： 题型：

已知函数f(x)＝－(a>0，x>0)．

(1)求证：f(x)在(0，＋∞)上是增加的；

(2)若f(x)在[，2]上的值域是[，2]，求a的值．

查看答案和解析>>

科目：高中数学 来源： 题型：

已知函数f(x)＝2x－b的零点为x₀，且x₀∈(－1,1)，那么b的取值范围是(　　)

A．(－2,2) B．(－1,1)

C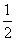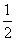．(－，) D．(－1,0)

查看答案和解析>>

科目：高中数学 来源： 题型：

用二分法求方程x³－2x－5＝0在区间(2,4)上的实数根时，取中点x₁＝3，则下一个有根区间是________．

查看答案和解析>>

科目：高中数学 来源： 题型：

某城市有甲，乙两家乒乓球俱乐部，两家设备和服务都很好，但收费方式不同．甲家每张球台每小时5元；乙家按月计费，一个月中30小时以内(含30小时)每张球台90元，超过30小时的部分每张球台每小时2元．小张准备下个月从这两家中的一家租一张球台开展活动，其活动时间不少于15小时，但不超过40小时．设在甲家租一张球台开展活动x小时的收费为f(x)元(15≤x≤40)，在乙家租一张球台开展活动x小时的收费为g(x)元(15≤x≤40)．

(1)求f(x)和g(x)；

(2)问：小张选择哪家比较合算？为什么？

查看答案和解析>>

科目：高中数学 来源： 题型：

计算下列各式的值：

log_2.56.25＋lg0.01＋ln＋2¹^＋log₂³；