
分析 (1)求出椭圆的焦点,即可求此抛物线的方程;
(2)根据韦达定理,求出|BC|,利用|BC|≤4,求b的取值范围.
解答 解:(1)椭圆4x2+2y2=1的焦点为$(0,\;\frac{1}{2})$,$(0,\;-\frac{1}{2})$,由题意得$\frac{p}{2}=\frac{1}{2}$,即p=1,
所以,该抛物线方程为x2=2y.…(2分)
(2)设B(x1,y1),C(x2,y2),
由$\left\{\begin{array}{l}\;y=-x+b\\ \;{x^2}=2y\end{array}\right.$得x2+2x-2b=0,…(3分)
根据题意△=4+8b>0,即$b>-\frac{1}{2}$.①…(4分)
又x1+x2=-2,x1x2=-2b,所以$|{BC}|=\sqrt{2}•|{\;{x_1}-{x_2}}|=\sqrt{2}•\sqrt{{{({x_1}+{x_2})}^2}-4{x_1}{x_2}}=\sqrt{2}•\sqrt{4+8b}$,
由于|BC|≤4,所以$\sqrt{2}•\sqrt{4+8b}≤4$,解得$b≤\frac{1}{2}$,…(7分)
再结合①式得$-\frac{1}{2}<b≤\frac{1}{2}$.…(8分)
点评 本题考查椭圆的方程与性质,考查抛物线的方程,考查直线与抛物线的位置关系,考查弦长的计算,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
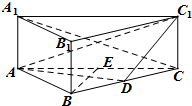 如图,三棱柱ABC-A1B1C1的侧棱垂直于底面,AB=BC=2AA1,∠ABC=90°,D是BC的中点,E是AC的中点
如图,三棱柱ABC-A1B1C1的侧棱垂直于底面,AB=BC=2AA1,∠ABC=90°,D是BC的中点,E是AC的中点查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $2\sqrt{2}$ | D. | $2\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com