
 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:高中数学 来源:2015届福建省高一上学期第一次月考数学试卷(解析版) 题型:解答题
20、 (本小题14分)
已知函数y=x2-2ax+1(a为常数)在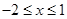 上的最小值为
上的最小值为 ,
,
试将 用a表示出来,并求出
用a表示出来,并求出 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年江苏省高三预测卷2数学 题型:解答题
(本小题满分14分)
如图,某市拟在道路的一侧修建一条运动赛道,赛道的前一部分为曲线段ABC,该曲线段为函数y= (A>0,
(A>0, >0,
>0,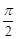 <
< <
<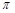 ),x∈[-3,0]的图象,且图象的最高点为B(-1,
),x∈[-3,0]的图象,且图象的最高点为B(-1,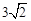 );赛道的中间部分为
);赛道的中间部分为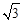 千米的水平跑到CD;赛道的后一部分为以O圆心的一段圆弧
千米的水平跑到CD;赛道的后一部分为以O圆心的一段圆弧 .
.

(1)求 ,
, 的值和∠DOE的值;
的值和∠DOE的值;
(2)若要在圆弧赛道所对应的扇形区域内建一个“矩形草坪”,如图所示,矩形的一边在道路AE上,一个顶点在扇形半径OD上.记∠POE= ,求当“矩形草坪”的面积最大时
,求当“矩形草坪”的面积最大时 的值.
的值.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年江苏省高三预测卷2数学 题型:解答题
(本小题满分14分)
如图,某市拟在道路的一侧修建一条运动赛道,赛道的前一部分为曲线段ABC,该曲线段为函数y= (A>0,
(A>0, >0,
>0, <
< <
< ),x∈[-3,0]的图象,且图象的最高点为B(-1,
),x∈[-3,0]的图象,且图象的最高点为B(-1, );赛道的中间部分为
);赛道的中间部分为 千米的水平跑到CD;赛道的后一部分为以O圆心的一段圆弧
千米的水平跑到CD;赛道的后一部分为以O圆心的一段圆弧 .
.

(1)求 ,
, 的值和∠DOE的值;
的值和∠DOE的值;
(2)若要在圆弧赛道所对应的扇形区域内建一个“矩形草坪”,如图所示,矩形的一边在道路AE上,一个顶点在扇形半径OD上.记∠POE= ,求当“矩形草坪”的面积最大时
,求当“矩形草坪”的面积最大时 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题14分)
设函数y=f(x)的定义域为(0,+∞),且在(0,+∞)上单调递增,若对任意x,y∈(0,+∞)都有:f(xy)=f(x)+f(y)成立,数列{an}满足:a1=f(1)+1,
(1)求数列{an}的通项公式,并求Sn关于n的表达式;
(2)设函数g(x)对任意x、y都有:g(x+y)=g(x)+g(y)+2xy,若g(1)=1,正项数列{bn}满足:,Tn为数列{bn}的前n项和,试比较4Sn与Tn的大小。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com