
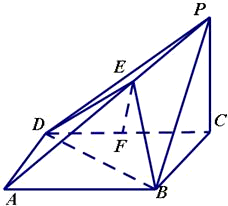
 如图四棱锥P-ABCD中,底面ABCD是平行四边形,PC⊥平面ABCD,F是DC的中点,
如图四棱锥P-ABCD中,底面ABCD是平行四边形,PC⊥平面ABCD,F是DC的中点,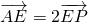 .
. ,
, PC=BC=2,求证:平面BDE⊥面PBC.
PC=BC=2,求证:平面BDE⊥面PBC.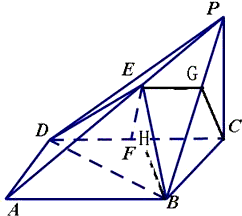 证明:(Ⅰ)直线EF与平面PBC相交.…(2分)
证明:(Ⅰ)直线EF与平面PBC相交.…(2分)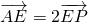 ,∴
,∴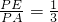 ,
,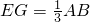 ,∵
,∵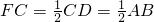 ,
, ,PC⊥平面ABCD,
,PC⊥平面ABCD,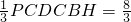 ,PC⊥BD.
,PC⊥BD.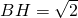 ,…(9分)
,…(9分) ,
, ,
, ,结合题中的条件可得
,结合题中的条件可得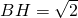 ,所以
,所以 ,所以BH=CH=HD,所以DB⊥BC.再利用面面垂直的判定定理可得面面垂直.
,所以BH=CH=HD,所以DB⊥BC.再利用面面垂直的判定定理可得面面垂直.

 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案科目:高中数学 来源: 题型:
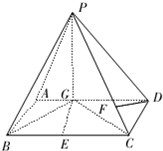 已知如图四棱锥P-ABCD中,底面ABCD是平行四边形,PG⊥平面ABC,垂足G在AD上,且AG=
已知如图四棱锥P-ABCD中,底面ABCD是平行四边形,PG⊥平面ABC,垂足G在AD上,且AG=| 1 |
| 3 |
| CF |
| CP |
查看答案和解析>>
科目:高中数学 来源:上海市模拟题 题型:解答题
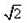 ,F是BC的中点.
,F是BC的中点.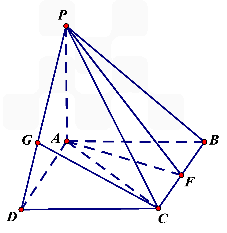
查看答案和解析>>
科目:高中数学 来源:浙江省模拟题 题型:解答题
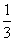 GD,GB⊥GC,GB=GC=2,PC=4,E是BC的中点.
GD,GB⊥GC,GB=GC=2,PC=4,E是BC的中点.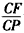 的值。
的值。 
查看答案和解析>>
科目:高中数学 来源: 题型:
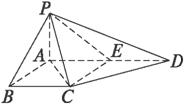
(1)三棱锥P—ACD的体积;
(2)直线PC与AB所成角的大小.
查看答案和解析>>
科目:高中数学 来源:2012年浙江省高考数学冲刺试卷A(理科)(解析版) 题型:解答题
 ,E是BC的中点.
,E是BC的中点. 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com