（09年丰台区期末文）（14分）
设椭圆M：
(a＞b＞0)的离心率为
，长轴长为
，设过右焦点F。
（Ⅰ）求椭圆M的方程；
（Ⅱ）设过右焦点F倾斜角为
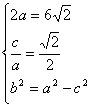
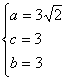的直线交椭M于A，B两点，求证| AB | =
。 解析：（Ⅰ）
所求椭圆M的方程为
…4分
（Ⅱ）当
≠
，设直线AB的斜率为k = tan，焦点F ( 3 , 0 )，则直线AB的方程为
y = k ( x 3 ) 有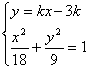
( 1 + 2k2 )x2 12k2x + 18( k2 1 ) = 0
设点A ( x1 , y1 ) , B ( x2 , y2 ) 有x1 + x2 =
, x1x2 =
|AB| =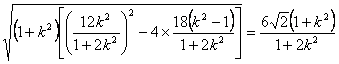
** … 7分
又因为 k = tan=
代入**式得
|AB| =
………… 10分
当=时，直线AB的方程为x = 3，此时|AB| =
……………… 12分
而当=时，|AB| =
=
……………………………………… 14分 
科目：高中数学 来源： 题型：
（09年丰台区期末文）（13分）
已知数列{an n }是等比数列，且满足a1 = 2 , an+1 = 3an 2n + 1 , n∈N*。
（Ⅰ）求数列{an}的通项公式an；
（Ⅱ）求数列{an}的前n项和Sn。
查看答案和解析>>
科目：高中数学 来源： 题型：
（09年丰台区期末文）（13分）
直四棱柱ABCD―A1B1C1D1中，∠ADC = 90°，△ABC为等边三角形，且AA1 = AD = DC
= 2 。
（Ⅰ）求异面直线AC1与BC所成的角余弦值；
（Ⅱ）求证：BD⊥平面AC1；
（Ⅲ）求二面角B―AC1―C的正切值。
查看答案和解析>>
科目：高中数学 来源： 题型：
（09年丰台区期末文）（14分）
已知甲盒内有大小相同的3个红球和4个黑球，乙盒内有大小相同的5个红球和4个黑球，现从甲、乙两个盒内各任取2个球。
（Ⅰ）求取出的4个球均为黑球的概率；
（Ⅱ）求取出的4个球中恰有一个红球的概率。
查看答案和解析>>
科目：高中数学 来源： 题型：
（09年丰台区期末文）（13分）
已知函数f ( x ) = x3 x2 x 。
（Ⅰ）求函数f ( x )在点( 2 , 2 )处的切线方程；
（Ⅱ）求函数f ( x )的极大值和极小值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com