
(09年丰台区期末文)(13分)
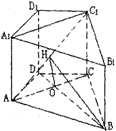
直四棱柱ABCD―A1B1C1D1中,∠ADC = 90°,△ABC为等边三角形,且AA1 = AD = DC
= 2 。
(Ⅰ)求异面直线AC1与BC所成的角余弦值;
(Ⅱ)求证:BD⊥平面AC1;
(Ⅲ)求二面角B―AC1―C的正切值。

解析:(Ⅰ)在直四棱柱ABCD―A1B1C1D1中,BC∥B1C1
∠AC1B1是异面直线AC1与BC所成的角 … 2分
 在△AC1B1中,AC1 = AB1 =
在△AC1B1中,AC1 = AB1 =![]() ,
,
C1B1 =![]() ,cos∠AC1B1 =
,cos∠AC1B1 =![]()
故 异面直线AC1与BC所成的角的余弦值为![]() ………………………… 4分
………………………… 4分
(Ⅱ)因为AD = DC , AB = BC 可得 BD⊥AC(垂直平分线)……… 5分
又 CC1⊥平面ABCD,AC为AC1平面ABCD上的射影 ………………… 7分
所以 BD⊥AC1 …………………………………………………………… 8分
(Ⅲ)设AC∩BD = O,由(Ⅱ)得 BD⊥平面ACC1,过O作OH⊥AC1,垂足为
H,连接BH,则BH⊥AC1,∠OHB为二面角B―AC1―C的平面角 … 11分
在Rt△OBH中,OB =![]() ,OH =
,OH =![]()
![]() tan∠OHB = 3 ………… 13分
tan∠OHB = 3 ………… 13分


 口算能手系列答案
口算能手系列答案科目:高中数学 来源: 题型:
(09年丰台区期末文)(14分)
设椭圆M:![]() (a>b>0)的离心率为
(a>b>0)的离心率为![]() ,长轴长为
,长轴长为![]() ,设过右焦点F。
,设过右焦点F。
(Ⅰ)求椭圆M的方程;
(Ⅱ)设过右焦点F倾斜角为查看答案和解析>>
科目:高中数学 来源: 题型:
(09年丰台区期末文)(13分)
已知数列{an n }是等比数列,且满足a1 = 2 , an+1 = 3an 2n + 1 , n∈N*。
(Ⅰ)求数列{an}的通项公式an;
(Ⅱ)求数列{an}的前n项和Sn。
查看答案和解析>>
科目:高中数学 来源: 题型:
(09年丰台区期末文)(14分)
已知甲盒内有大小相同的3个红球和4个黑球,乙盒内有大小相同的5个红球和4个黑球,现从甲、乙两个盒内各任取2个球。
(Ⅰ)求取出的4个球均为黑球的概率;
(Ⅱ)求取出的4个球中恰有一个红球的概率。
查看答案和解析>>
科目:高中数学 来源: 题型:
(09年丰台区期末文)(13分)
已知函数f ( x ) = x3 x2 x 。
(Ⅰ)求函数f ( x )在点( 2 , 2 )处的切线方程;
(Ⅱ)求函数f ( x )的极大值和极小值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com