
【题目】在甲、乙等7个选手参加的一次演讲比赛中,采用抽签的方式随机确定每个选手的演出顺序(序号为1,2,……7),求:
(1)甲、乙两个选手的演出序号至少有一个为奇数的概率;
(2)甲、乙两选手之间的演讲选手个数![]() 的分布列与期望.
的分布列与期望.
 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案科目:高中数学 来源: 题型:
【题目】以下关于投影的叙述不正确的是( )
A. 手影就是一种投影
B. 中心投影的投影线相交于点光源
C. 斜投影的投影线不平行
D. 正投影的投影线和投影面垂直
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】用0,1,2,3,4组成没有重复数字的全部五位数中,若按从小到大的顺序排列,则数字12340应是第( )个数.
A.6 B.9 C.10 D.8
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】两平行线分别经过点A(5,0),B(0,12),它们之间的距离d满足的条件是( )
A.0<d≤5
B.0<d≤13
C.0<d<12
D.5≤d≤12
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在边长为1的等边三角形![]() 中,
中,![]() 分别是
分别是![]() 边上的点,
边上的点,![]() ,
,![]() 是
是![]() 的中点,
的中点,![]() 与
与![]() 交于点
交于点![]() ,将
,将![]() 沿
沿![]() 折起,得到如图2所示的三棱锥
折起,得到如图2所示的三棱锥![]() ,其中
,其中![]() .
.
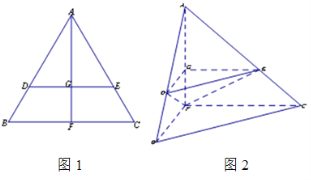
(1) 证明:![]() //平面
//平面![]() ;
;
(2) 证明:![]()
![]() 平面
平面![]() ;
;
(3) 当![]() 时,求三棱锥
时,求三棱锥![]() 的体积
的体积![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在等比数列{an}中,a1=2,a3,a2+a4,a5成等差数列.
(1)求数列{an}的通项公式;
(2)若数列{bn}满足b1+![]() +…+
+…+![]() =an(n∈N*),{bn}的前n项和为Sn,求使Sn﹣nan+6≥0成立的正整数n的最大值.
=an(n∈N*),{bn}的前n项和为Sn,求使Sn﹣nan+6≥0成立的正整数n的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,平面
中,平面![]() 平面
平面![]() ,
,![]() ,
,![]() 是等边三角形.已知
是等边三角形.已知![]() ,
,![]() ,
,![]() .
.
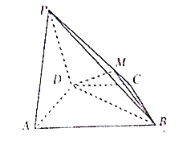
(1)设![]() 是
是![]() 上的一点,证明:平面
上的一点,证明:平面![]() 平面
平面![]() ;
;
(2)当![]() 点位于线段
点位于线段![]() 什么位置时,
什么位置时,![]() 平面
平面![]() ?
?
(3)求四棱锥![]() 的体积.
的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com