Question

【题目】已知椭圆．

（Ⅰ）求椭圆的离心率；

（Ⅱ）设为坐标原点，为椭圆上的三个动点，若四边形为平行四边形，判断的面积是否为定值，并说明理由．

Answer 1

【答案】（Ⅰ）；（Ⅱ）的面积为定值.

【解析】

试题分析：（Ⅰ）由已知，椭圆的标准方程为，则离心率；（Ⅱ）由已知，的面积等于的面积，分情况：若是椭圆的右顶点，的面积；若不是椭圆的左、右顶点，可设，，则由四边形为平行四边形，得，即，联立方程由韦达定理知，又到的距离，所以的面积.

试题解析：（Ⅰ）椭圆的标准方程为：

所以。

所以椭圆的离心率。

（Ⅱ）①若是椭圆的右顶点（左顶点一样），此时垂直平方。

所以。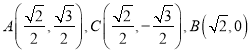

所以的面积。

②若不是椭圆的左、右顶点，设，

，

由得，

，

。

因为四边形为平行四边形，

所以。

所以，

代入椭圆方程，化简得。

因为

。

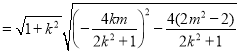
点到的距离。

所以的面积。

综上，的面积为定值。

因为的面积等于的面积，

所以的面积为定值。