
在 中,角
中,角 所对的边分别为
所对的边分别为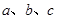 ,已知
,已知 ,
,
(Ⅰ)求 的大小;
的大小;
(Ⅱ)若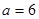 ,求
,求 的取值范围.
的取值范围.
 核心素养学练评系列答案
核心素养学练评系列答案科目:高中数学 来源: 题型:解答题
钓鱼岛及其附属岛屿是中国固有领土,如图:点A、B、C分别表示钓鱼岛、南小岛、黄尾屿,点C在点A的北偏东47°方向,点B在点C的南偏西36°方向,点B在点A的南偏东79°方向,且A、B两点的距离约为3海里.
(1)求A、C两点间的距离;(精确到0.01)
(2)某一时刻,我国一渔船在A点处因故障抛锚发出求救信号.一艘R国舰艇正从点C正东10海里的点P处以18海里/小时的速度接近渔船,其航线为P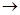 C
C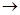 A(直线行进),而我东海某渔政船正位于点A南偏西60°方向20海里的点Q处,收到信号后赶往救助,其航线为先向正北航行8海里至点M处,再折向点A直线航行,航速为22海里/小时.渔政船能否先于R国舰艇赶到进行救助?说明理由.
A(直线行进),而我东海某渔政船正位于点A南偏西60°方向20海里的点Q处,收到信号后赶往救助,其航线为先向正北航行8海里至点M处,再折向点A直线航行,航速为22海里/小时.渔政船能否先于R国舰艇赶到进行救助?说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,海上有 两个小岛相距10
两个小岛相距10 ,船O将保持观望A岛和B岛所成的视角为
,船O将保持观望A岛和B岛所成的视角为 ,现从船O上派下一只小艇沿
,现从船O上派下一只小艇沿 方向驶至
方向驶至 处进行作业,且
处进行作业,且 .设
.设
 。
。
(1)用 分别表示
分别表示 和
和 ,并求出
,并求出 的取值范围;
的取值范围;
(2)晚上小艇在 处发出一道强烈的光线照射A岛,B岛至光线
处发出一道强烈的光线照射A岛,B岛至光线 的距离为
的距离为 ,求BD的最大值.
,求BD的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,甲船以每小时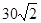 海里的速度向正北方航行,乙船按固定方向匀速直线航行,当甲船位于
海里的速度向正北方航行,乙船按固定方向匀速直线航行,当甲船位于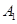 处时,乙船位于甲船的北偏西
处时,乙船位于甲船的北偏西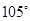 方向的
方向的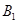 处,此时两船相距
处,此时两船相距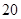 海里,当甲船航行
海里,当甲船航行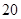 分钟到达
分钟到达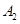 处时,乙船航行到甲船的北偏西
处时,乙船航行到甲船的北偏西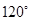 方向的
方向的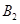 处,此时两船相距
处,此时两船相距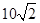 海里,问乙船每小时航行多少海里?
海里,问乙船每小时航行多少海里?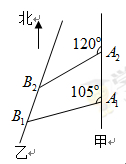
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com