
在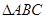 中,
中,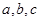 分别为内角A,B,C所对的边长,
分别为内角A,B,C所对的边长,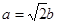 ,
,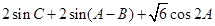
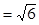 .
.
(1)求角B的大小。
(2)若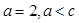 求
求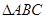 的面积
的面积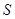 .
.
(1)角B为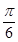 ;(2)
;(2)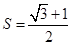 .
.
解析试题分析:本题考查解三角形中的正弦定理的运用以及运用三角公式进行三角变换的能力和三角形面积公式,考查基本的运算能力.第一问,由正弦定理得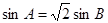 ,再利用两角和与差的正弦公式和倍角公式化简第二个已知条件,两式结合,得
,再利用两角和与差的正弦公式和倍角公式化简第二个已知条件,两式结合,得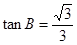 ,注意是在三角形中求角
,注意是在三角形中求角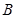 ;第二问,结合第一问的结论,得
;第二问,结合第一问的结论,得 ,通过边的大小确定角
,通过边的大小确定角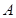 的大小,已知有
的大小,已知有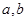 边的长度,要求三角形面积还需求
边的长度,要求三角形面积还需求 角,由
角,由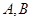 角求
角求 角,从而求出
角,从而求出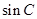 ,所以代入三角形面积公式中即可.
,所以代入三角形面积公式中即可.
试题解析:(1)由正弦定理及已知可得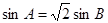 1分
1分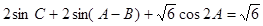 得
得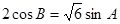 4分
4分
所以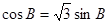 解得
解得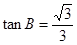 又因为在
又因为在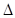 ABC中
ABC中
所以角B为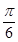 6
6 分
分
(2)由(1)知 又因为
又因为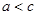 所以
所以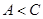 7分
7分
所以
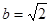
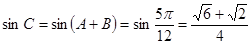 9分
9分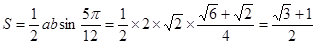 12分
12分
考点:1.正弦定理;2.两角和与差的正弦公式;3.三角形面积公式.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
在△ABC中,a、b、c分别为角A、B、C的对边,4sin2 -cos 2A=
-cos 2A= .
.
(1)求角A的度数;
(2)若a= ,b+c=3,求△ABC的面积.
,b+c=3,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,甲船以每小时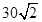 海里的速度向正北方航行,乙船按固定方向匀速直线航行,当甲船位于
海里的速度向正北方航行,乙船按固定方向匀速直线航行,当甲船位于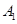 处时,乙船位于甲船的北偏西
处时,乙船位于甲船的北偏西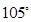 方向的
方向的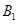 处,此时两船相距
处,此时两船相距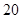 海里,当甲船航行
海里,当甲船航行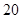 分钟到达
分钟到达 处时,乙船航行到甲船的北偏西
处时,乙船航行到甲船的北偏西 方向的
方向的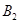 处,此时两船相距
处,此时两船相距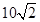 海里,问乙船每小时航行多少海里?
海里,问乙船每小时航行多少海里?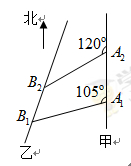
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,山顶有一座石塔 ,已知石塔的高度为
,已知石塔的高度为 .
.
(Ⅰ)若以 为观测点,在塔顶
为观测点,在塔顶 处测得地面上一点
处测得地面上一点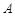 的俯角为
的俯角为 ,在塔底
,在塔底 处测得
处测得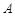 处的俯角为
处的俯角为 ,用
,用 表示山的高度
表示山的高度 ;
;
(Ⅱ)若将观测点选在地面的直线 上,其中
上,其中 是塔顶
是塔顶 在地面上的射影.已知石塔高度
在地面上的射影.已知石塔高度 ,当观测点
,当观测点 在
在 上满足
上满足 时看
时看 的视角(即
的视角(即 )最大,求山的高度
)最大,求山的高度 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
在△ABC中,内角A,B,C的对边分别为a,b,c,且满足 (a-c)cosB=bcosC.
(1)求角B的大小;(2)若b=,求△ABC面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com