练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知向量m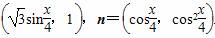＝ (1)若m·n＝1，求cos的值；

    (2)记f(x)＝m·n，在△ABC中，角A，B，C的对边分别是a，b，c，且满足(2a－c)cos B＝bcos C，求函数f(A)的取值范围．


     (2)因为(2a－c)cos B＝bcos C，

    由正弦定理得(2sin A－sin C)cos B＝sin Bcos C，

    即2sin Acos B－sin Ccos B＝sin Bcos C，

    所以2sin Acos B＝sin(B＋C)，(8分)

    又因为A＋B＋C＝π，

    所以sin(B＋C)＝sin A，且sin A≠0，


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


     “1<x<2”是“x<2”成立的(　　)

      A.充分不必要条件  B.必要不充分条件  C.充分必要条件  D.既不充分也不必要条件

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设，求的值。

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知函数，且函数的最小正周期为。

    （I）求函数的解析式；

    （II）在中，角A,B,C所对的边分别为a,b,c，若的值。

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    在等腰梯形ABCD中，AB∥CD，AB＝BC＝AD＝2，CD＝4，E为边DC的中点，如图1.将△ADE沿AE折起到△AEP位置，连PB、PC，点Q是棱AE的中点，点M在棱PC上，如图2.

    (1)若PA∥平面MQB，求PM∶MC；

    (2)若平面AEP⊥平面ABCE，点M是PC的中点，求三棱锥A ­MQB的体积．

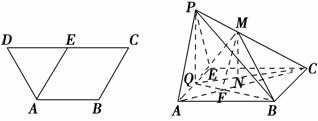
    图1　　　　　　　　图2　　

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设数列{bn}满足bn＋2＝－bn＋1－bn(n∈N*)，b2＝2b1.

    (1)若b3＝3，求b1的值；

    (2)求证数列{bnbn＋1bn＋2＋n}是等差数列；

    (3)设数列{Tn}满足：Tn＋1＝Tnbn＋1(n∈N*)，且T1＝b1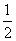＝－，若存在实数p，q，对任意n∈N*都有p≤T1＋T2＋T3＋…＋Tn＜q成立，试求q－p的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    在△ABC中，角A，B，C的对边分别为a，b，c，且c＝2，C＝60°.

    (1)求的值；

    (2)若a＋b＝ab，求△ABC的面积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知两圆相交于A（1，3）、B（-3，-1）两点，且两圆的圆心都在直线y=mx+n上，则m+n=

                  。

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    的展开式中的系数为         ．

    查看答案和解析>>

    同步练习册答案