
【题目】已知函数f(x)=xlnx.
(1)求f(x)的单调区间和极值;
(2)若对任意 ![]() 恒成立,求实数m的最大值.
恒成立,求实数m的最大值.
【答案】
(1)解:∵f(x)=xlnx,
∴f'(x)=lnx+1,
∴f'(x)>0有 ![]() ,∴函数f(x)在
,∴函数f(x)在 ![]() 上递增,f'(x)<0有
上递增,f'(x)<0有 ![]() ,
,
∴函数f(x)在 ![]() 上递减,
上递减,
∴f(x)在 ![]() 处取得极小值,极小值为
处取得极小值,极小值为 ![]()
(2)解:∵2f(x)≥﹣x2+mx﹣3
即mx≤2xlnx+x2+3,又x>0,
∴ ![]() ,
,
令 ![]() ,
,
![]()
令h'(x)=0,解得x=1或x=﹣3(舍)
当x∈(0,1)时,h'(x)<0,函数h(x)在(0,1)上递减
当x∈(1,+∞)时,h'(x)>0,函数h(x)在(1,+∞)上递增,
∴h(x)min=h(1)=4.
∴m≤4,
即m的最大值为4.
【解析】(1)求函数的导数,利用函数单调性和极值之间的关系即可求f(x)的单调区间和极值;(2)利用不等式恒成立,进行参数分离,利用导数即可求出实数m的最大值.


科目:高中数学 来源: 题型:
【题目】已知数列{an}满足条件(n﹣1)an+1=(n+1)(an﹣1),且a2=6,
(1)计算a1、a3、a4 , 请猜测数列{an}的通项公式并用数学归纳法证明;
(2)设bn=an+n(n∈N*),求 ![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱柱ABCD﹣A1B1C1D1中,侧棱A1A⊥底面ABCD,AB∥DC,AB⊥AD,AD=CD=1,AA1=AB=2,E为棱AA1的中点. 
(1)证明B1C1⊥CE;
(2)求二面角B1﹣CE﹣C1的正弦值.
(3)设点M在线段C1E上,且直线AM与平面ADD1A1所成角的正弦值为 ![]() ,求线段AM的长.
,求线段AM的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随机抽取某中学甲乙两班各6名同学,测量他们的身高(单位:cm),获得身高数据的茎叶图如图,则甲班样本数据的众数和乙班样本数据的中位数分别是( ) 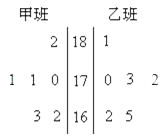
A.170,170
B.171,171
C.171,170
D.170,172
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数y=f(x)对于任意x∈R有 ![]() ,且当x∈[﹣1,1]时,f(x)=x2+1,则以下命题正确的是: ①函数数y=f(x)是周期为2的偶函数;
,且当x∈[﹣1,1]时,f(x)=x2+1,则以下命题正确的是: ①函数数y=f(x)是周期为2的偶函数;
②函数y=f(x)在[2,3]上单调递增;
③函数 ![]() 的最大值是4;
的最大值是4;
④若关于x的方程[f(x)]2﹣f(x)﹣m=0有实根,则实数m的范围是[0,2];
⑤当x1 , x2∈[1,3]时, ![]() .
.
其中真命题的序号是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若数列{an}是等差数列,首项a1>0,a2003+a2004>0,a2003 . a2004<0,则使前n项和Sn>0成立的最大自然数n是( )
A.4005
B.4006
C.4007
D.4008
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数y=f(x)是定义在(0,+∞)上的函数,并且满足下面三个条件: ①对任意正数x,y,都有f(xy)=f(x)+f(y);
②当x>1时,f(x)>0;
③f(3)=1,
(1)求f(1), ![]() 的值;
的值;
(2)判断函数f(x)在区间(0,+∞)上单调性,并用定义给出证明;
(3)对于定义域内的任意实数x,f(kx)+f(4﹣x)<2(k为常数,且k>0)恒成立,求正实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题p:“ ![]() =1是焦点在x轴上的椭圆的标准方程”,命题q:“不等式组
=1是焦点在x轴上的椭圆的标准方程”,命题q:“不等式组  所表示的区域是三角形”.若p∨q为真命题,p∧q为假命题,求实数m的取值范围.
所表示的区域是三角形”.若p∨q为真命题,p∧q为假命题,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设直线l的方程是x+my+2 ![]() =0,圆O的方程是x2+y2=r2(r>0).
=0,圆O的方程是x2+y2=r2(r>0).
(1)当m取一切实数时,直线l与圆O都有公共点,求r的取值范围;
(2)r=5时,求直线l被圆O截得的弦长的取值范围;
(3)当r=1时,设圆O与x轴相交于P,Q两点,M是圆O上异于P,Q的任意一点,直线PM交直线l′:x=3于点P′,直线QM交直线l′于点Q′.求证:以P′Q′为直径的圆C总经过定点,并求出定点坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com