
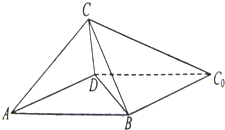
 如图,一张平行四边形的硬纸片ABC0D中,AD=BD=1,AB=
如图,一张平行四边形的硬纸片ABC0D中,AD=BD=1,AB=| 2 |
| 1 |
| 2 |
| ||
| 2 |
| DA |
| BC |
| 2 |
| 2 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| DA |
| BC |
| DA |
| BC |
| 1 |
| 2 |
| ||
| 2 |
| DA |
| BC |
| ||||
|
|
| 1 |
| 2 |
| DA |
| BC |


 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案科目:高中数学 来源: 题型:
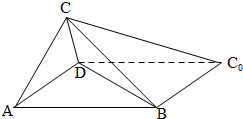 如图,一张平行四边形的硬纸片ABC0D中,AD=BD=1,AB=
如图,一张平行四边形的硬纸片ABC0D中,AD=BD=1,AB=| 2 |
查看答案和解析>>
科目:高中数学 来源:2012届度湖南省高三下学期二轮复习理科数学试卷 题型:解答题
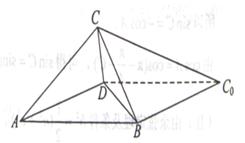
如图,一张平行四边形的硬纸片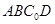 中,
中,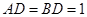 ,
, 。沿它的对角线
。沿它的对角线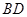 把△
把△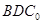 折起,使点
折起,使点 到达平面
到达平面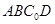 外点
外点 的位置。
的位置。
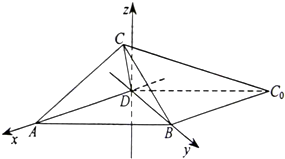
(Ⅰ)△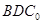 折起的过程中,判断平面
折起的过程中,判断平面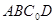 与平面
与平面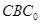 的位置关系,并给出证明;
的位置关系,并给出证明;
(Ⅱ)当△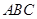 为等腰三角形,求此时二面角
为等腰三角形,求此时二面角 的大小。
的大小。
查看答案和解析>>
科目:高中数学 来源:河北省2009-2010学年度第二学期二调考试高一年级数学试卷理科 题型:解答题
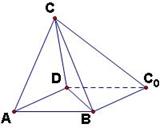
(本小题共12分)如图,一张平行四边形的硬纸片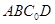 中,
中,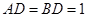 ,
,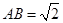 。沿它的对角线
。沿它的对角线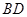 把△
把△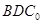 折起,使点
折起,使点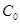 到达平面
到达平面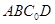 外点
外点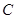 的位置。
的位置。
(Ⅰ)证明:平面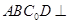 平面
平面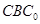 ;
;
(Ⅱ)如果△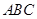 为等腰三角形,求二面角
为等腰三角形,求二面角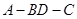 的大小。
的大小。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com