
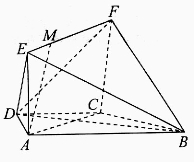
(本小题12分)如图,在梯形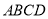 中,
中,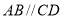 ,
,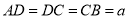 ,
,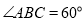 ,四边形
,四边形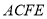 是矩形,且平面
是矩形,且平面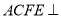 平面
平面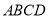 ,点
,点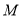 在线段
在线段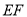 上.
上.
(1)求证: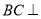 平面
平面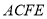 ;
;
(2)当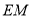 为何值时,
为何值时,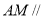 平面
平面 ?证明你的结论.
?证明你的结论.
(1)证明见解析;(2)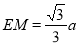 ,
,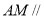 平面
平面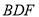 ,证明见解析
,证明见解析
【解析】
试题分析:(1)证明线面垂直的方法:一是线面垂直的判定定理;二是利用面面垂直的性质定理;三是平行线法(若两条平行线中的一条垂直于这个平面,则另一条也垂直于这个平面.解题时,注意线线、线面与面面关系的相互转化;(2)证明线面平行常用方法:一是利用线面平行的判定定理,二是利用面面平行的性质定理,三是利用面面平行的性质;(3)证明两个平面垂直,首先考虑直线与平面垂直,也可以简单记为“证面面垂直,找线面垂直”,是化归思想的体现,这种思想方法与空间中的平行关系的证明类似,掌握化归与转化思想方法是解决这类题的关键.
试题解析:(1)在梯形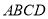 中,
中,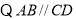 ,
, 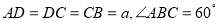 ,
,
 四边形
四边形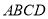 是等腰梯形,
是等腰梯形,
且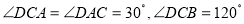 ,
,
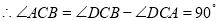 ,
,
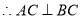 . 3分
. 3分
又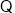 平面
平面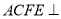 平面
平面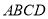 ,交线为
,交线为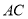 ,
,
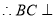 平面
平面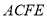 . 6分
. 6分
(2)当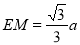 时,
时,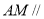 平面
平面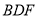 , 7分
, 7分
在梯形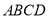 中,设
中,设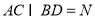 ,连接
,连接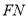 ,则
,则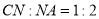 ,
,
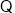
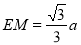 ,而
,而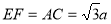 ,
, , 9分
, 9分
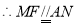 ,
, 四边形
四边形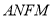 是平行四边形,
是平行四边形,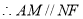 ,
,
又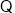
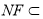 平面
平面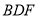 ,
,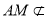 平面
平面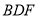
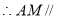 平面
平面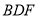 . 12分
. 12分
考点:1、直线与平面垂直的判定;2、直线与平面平行的判定.


 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案科目:高中数学 来源:2014-2015学年宁夏银川市高三上学期期中考试文科数学试卷(解析版) 题型:选择题
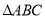 的内角
的内角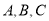 的对边分别为
的对边分别为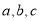 已知
已知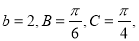 则
则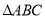 的面积为( )
的面积为( )
A.2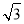 +2 B.
+2 B.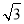 +1 C.2
+1 C.2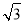 -2 D.
-2 D.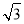 -1
-1
查看答案和解析>>
科目:高中数学 来源:2014-2015学年湖南省浏阳、醴陵、攸县三校高三联考理科数学试卷(解析版) 题型:选择题
已知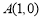 ,曲线
,曲线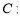
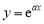 恒过点
恒过点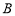 ,若
,若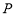 是曲线
是曲线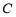 上的动点,且
上的动点,且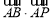 的最小值为
的最小值为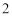 ,则
,则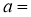 ( ).
( ).
A.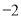 B.-1 C.2 D.1
B.-1 C.2 D.1
查看答案和解析>>
科目:高中数学 来源:2014-2015学年湖南省浏阳、醴陵、攸县三校高三联考理科数学试卷(解析版) 题型:选择题
已知集合A={0,1,2,3},B={x|x=2a,a∈A},则A∩B中元素的个数为( )
A.0 B.1 C.2 D.3
查看答案和解析>>
科目:高中数学 来源:2014-2015学年河北省保定市高三上学期12月份联考文科数学试卷(解析版) 题型:选择题
从抛物线y2= 4x上一点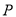 引抛物线准线的垂线,垂足为
引抛物线准线的垂线,垂足为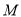 ,且
,且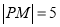 ,设抛物线的焦点为
,设抛物线的焦点为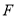 ,则△
,则△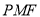 的面积为( )
的面积为( )
A.5 B.10 C.20 D.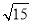
查看答案和解析>>
科目:高中数学 来源:2014-2015学年安徽省江淮名校高三第二次联考理科数学试卷(解析版) 题型:填空题
若正实数a使得不等式|2x - a|+|3x- 2a|≥a2对任意实数x恒成立,则实数a的范围是 。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com