
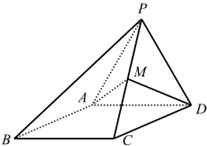
 如图,四棱锥P-ABCD,侧面PAD是边长为2的正三角形,且与底面垂直,底面ABCD是∠ABC=60°的菱形,M为PC的中点.
如图,四棱锥P-ABCD,侧面PAD是边长为2的正三角形,且与底面垂直,底面ABCD是∠ABC=60°的菱形,M为PC的中点.分析 (1)取AD的中点O,连结OP,OC,证明AD⊥平面OPC即可得出PC⊥AD;
(2)取OC的中点N,连结MN,DN,可证MN⊥平面ABCD,故而∠MDN为DM与平面ABCD所成的角,利用勾股定理计算DN,DM得出cos∠MDN.
解答  解:(1)取AD的中点O,连结OP,OC,
解:(1)取AD的中点O,连结OP,OC,
∵底面ABCD是∠ABC=60°的菱形,
∴△ACD是等边三角形,
又侧面PAD是边长为2的正三角形,O为AD的中点,
∴OP⊥AD,OC⊥AD,
又OP?平面OPC,OC?平面OPC,OP∩OC=O,
∴AD⊥平面OPC,又PC?平面OPC,
∴AD⊥PC.
(2)取OC的中点N,连结MN,DN,
∵平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,OP⊥AD,
∴OP⊥平面ABCD,
∵M,N分别是PC,OC的中点,
∴MN∥PO,
∴MN⊥平面ABCD,
∴∠MDN为DM与平面ABCD所成的角,
∵△APD,△ACD是边长为2的等边三角形,
∴OC=OP=$\sqrt{3}$,OD=1,∴MN=ON=$\frac{\sqrt{3}}{2}$,
∴DN=$\sqrt{O{N}^{2}+O{D}^{2}}$=$\frac{\sqrt{7}}{2}$,∴DM=$\sqrt{M{N}^{2}+D{N}^{2}}$=$\frac{\sqrt{10}}{2}$.
∴cos∠MDN=$\frac{DN}{DM}$=$\frac{\sqrt{70}}{10}$.
点评 本题考查了线面垂直的判定与性质,线面角的计算,属于中档题.


 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{4}{5}$,$\frac{3}{5}$) | B. | (-1,$\frac{3}{5}$) | C. | ($\frac{3}{5}$,$\frac{4}{5}$) | D. | ($\frac{3}{5}$,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com