
分析 (I)根据对数函数的图象和性质,结合函数图象的平移变换,可得函数f(x)=2+log${\;}_{\frac{1}{2}}$x的草图;
(Ⅱ)将x=$\frac{1}{4}$代入,可得答案;
(Ⅲ)当-1<f(x)≤3时,-1<2+log${\;}_{\frac{1}{2}}$x≤3,解得答案.
解答 解:(I)函数f(x)=2+log${\;}_{\frac{1}{2}}$x的草图如下图所示:
(Ⅱ)当x=$\frac{1}{4}$时,f($\frac{1}{4}$)=2+log${\;}_{\frac{1}{2}}$$\frac{1}{4}$=4.
(Ⅲ)当-1<f(x)≤3时,-1<2+log${\;}_{\frac{1}{2}}$x≤3,
即-3<log${\;}_{\frac{1}{2}}$x≤1,
即$\frac{1}{2}$≤x<8.
点评 本题考查的知识点是对数函数的图象和性质,熟练掌握对数函数的图象和性质,是解答的关键.


 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
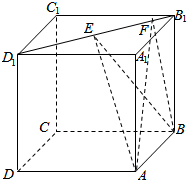 如图,正方体ABCD-A1B1C1D1的棱长为1,线段B1D1上有两个动点E、F,且EF=$\frac{1}{2}$,则下列结论中正确的序号是①②③.
如图,正方体ABCD-A1B1C1D1的棱长为1,线段B1D1上有两个动点E、F,且EF=$\frac{1}{2}$,则下列结论中正确的序号是①②③.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $9+\frac{π^2}{9}$ | B. | $9-\frac{π^2}{9}$ | C. | $4+\frac{π^2}{4}$ | D. | $4-\frac{π^2}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1 | B. | $\frac{{y}^{2}}{4}$+$\frac{{x}^{2}}{3}$=1 | C. | $\frac{{y}^{2}}{9}$+$\frac{{x}^{2}}{8}$=1 | D. | $\frac{{x}^{2}}{7}$+$\frac{{y}^{2}}{8}$=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\sqrt{2}$ | D. | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com