

| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| OC |
| AB |
| OC |
| AB |
| ||
| 5 |
| ||
| 5 |
| n |
| AC |
| AB |
|
| n |
| OB |
| n |
| OB |
| ||
| 6 |
| GH |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| GH |
| n |
| 1 |
| 2 |


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:高中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
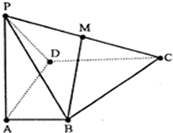
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
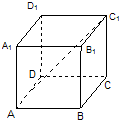
A.
| B.
| C.
| D.
|
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 2 |

查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
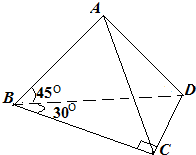
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 2 |
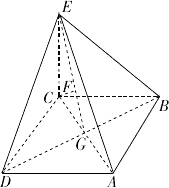
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 与
与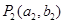 是直线y=kx+1(k为常数)上两个不同的点,则关于x和y的方程组
是直线y=kx+1(k为常数)上两个不同的点,则关于x和y的方程组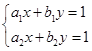 的解的情况是( )
的解的情况是( )A.无论k,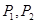 如何,总是无解 如何,总是无解 | B.无论k,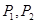 如何,总有唯一解 如何,总有唯一解 |
C.存在k,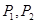 ,使之恰有两解 ,使之恰有两解 | D.存在k,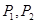 ,使之有无穷多解 ,使之有无穷多解 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com