
下列命题中:①在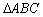 中,若
中,若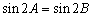 ,则
,则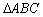 是等腰直角三角形;
是等腰直角三角形;
②奇函数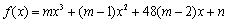 在区间
在区间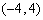 上是单调减函数.
上是单调减函数.
③如果正实数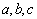 满足
满足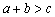 ,则
,则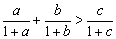 ;
;
④设数列{an}的前n项和为Sn,且an为复数isin 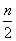 +cos
+cos 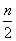 (n∈N*)的虚部,则S2 014=1
(n∈N*)的虚部,则S2 014=1
⑤复数 ,若(z1-z2)2+(z2-z3)2=0 则z1=z2=z3;
,若(z1-z2)2+(z2-z3)2=0 则z1=z2=z3;
其中正确的命题是
科目:高中数学 来源: 题型:
已知函数f(x)=x3+ax2+bx. 若y=f(x)的导数f′(x)对x∈[-1,1]都有f′(x)≤2,则 的范围 ( )
的范围 ( )
A.(-2,1] B.(-∞,-2)∪[1,+∞). C.( , 1]. D. [-2,
, 1]. D. [-2, ]
]
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数f(x)=x3+mx2+nx-2的图象过点(-1,-6),且函数g(x)=f′(x)+6x的图象关于y轴对称.
(1)求m,n的值及函数y=f(x)的单调区间;
(2)若a>0,求函数y=f(x)在区间(a-1,a+1)内的极值.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知曲线 ,直线
,直线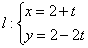 (
( 为参数)
为参数)
(1)写出曲线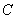 的参数方程,直线
的参数方程,直线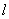 的普通方程;
的普通方程;
(2)过曲线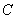 上任意一点
上任意一点 作与
作与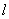 夹角为30°的直线,交
夹角为30°的直线,交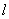 于点
于点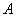 ,学科网求
,学科网求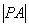 的最大值与最小值.
的最大值与最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
如图,四棱锥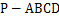 的底面
的底面 是平行四边形,
是平行四边形, ,
, ,
,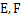 分别是棱
分别是棱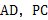 的中点.
的中点.
证明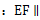 平面
平面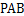 ;
;
若二面角P-AD-B为 ,
,
证明:平面PBC⊥平面ABCD
求直线EF与平面PBC所成角的正弦值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com