
已知函数f(x)=x3+mx2+nx-2的图象过点(-1,-6),且函数g(x)=f′(x)+6x的图象关于y轴对称.
(1)求m,n的值及函数y=f(x)的单调区间;
(2)若a>0,求函数y=f(x)在区间(a-1,a+1)内的极值.
解析:(1)由函数f(x)的图象过点(-1,-6),得m-n=-3.①
由f(x)=x3+mx2+nx-2,得f′(x)=3x2+2mx+n,
则g(x)=f′(x)+6x=3x2+(2m+6)x+n.
而g(x)的图象关于y轴对称,所以m=-3.代入①得n=0.
于是f′(x)=3x2-6x=3x(x-2).
由f′(x)>0得x>2或x<0,由f′(x)<0,得0<x<2,
∴f(x)的单调递增区间是(-∞,0)和(2,+∞);f(x)的单调递减区间是(0,2).(注:用∪扣2分)
(2)由(1)得
①当0<a<1时,f(x)在(a-1,a+1)内有极大值f(0)=-2,无极小值;
②当a=1时,f(x)在(a-1,a+1)内无极值;
③当1<a<3时,f(x)在(a-1,a+1)内有极小值f(2)=-6,无极大值;
④当a≥3时,f(x)在(a-1,a+1)内无极值.
综上得,当0<a<1时,f(x)有极大值-2,无极小值;
当1<a<3时,f(x)有极小值-6,无极大值;
当a=1或a≥3时,f(x)无极值.


 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案科目:高中数学 来源: 题型:
下列命题中:①在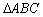 中,若
中,若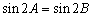 ,则
,则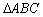 是等腰直角三角形;
是等腰直角三角形;
②奇函数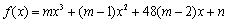 在区间
在区间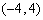 上是单调减函数.
上是单调减函数.
③如果正实数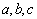 满足
满足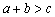 ,则
,则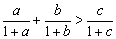 ;
;
④设数列{an}的前n项和为Sn,且an为复数isin 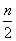 +cos
+cos 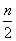 (n∈N*)的虚部,则S2 014=1
(n∈N*)的虚部,则S2 014=1
⑤复数 ,若(z1-z2)2+(z2-z3)2=0 则z1=z2=z3;
,若(z1-z2)2+(z2-z3)2=0 则z1=z2=z3;
其中正确的命题是
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com