
已知动点 到点
到点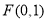 的距离等于点
的距离等于点 到直线
到直线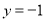 的距离,点
的距离,点 的轨迹为
的轨迹为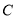 .
.
(Ⅰ)求轨迹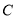 的方程;
的方程;
(Ⅱ)设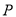 为直线
为直线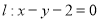 上的点,过点
上的点,过点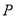 作曲线
作曲线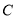 的两条切线
的两条切线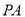 ,
, ,
,
(ⅰ)当点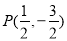 时,求直线
时,求直线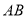 的方程;
的方程;
(ⅱ)当点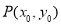 在直线
在直线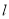 上移动时,求
上移动时,求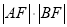 的最小值.
的最小值.
(Ⅰ) 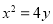 ;(Ⅱ)
;(Ⅱ)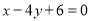 ,
,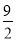
【解析】
试题分析:(Ⅰ)依题意,由抛物线定义知轨迹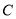 的方程为
的方程为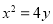 ,或设
,或设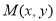 ,依题意:
,依题意: 
即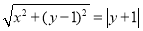 化简得
化简得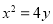 ;(Ⅱ)(ⅰ)易得切线
;(Ⅱ)(ⅰ)易得切线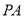 的方程为
的方程为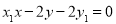 ,切线
,切线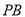 的方程为
的方程为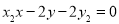 ,因切线
,因切线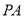 ,
,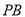 均过点
均过点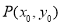 ,所以
,所以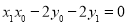 ,
,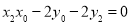 ,所以直线
,所以直线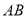 的方程为
的方程为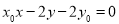 ,当点
,当点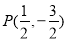 时,直线
时,直线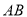 的方程为
的方程为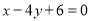 ;(ⅱ)由抛物线定义得
;(ⅱ)由抛物线定义得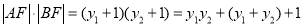 ,联立方程
,联立方程 得
得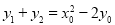 ,
,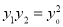 ,
,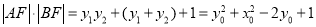
又点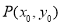 在直线
在直线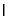 上,所以
上,所以 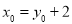 ,所以
,所以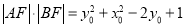

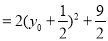 ,当
,当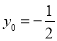 时,
时,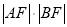 取得最小值
取得最小值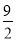
试题解析:法一:(Ⅰ)依题意,由抛物线定义知轨迹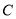 的方程为
的方程为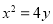 4分
4分
(Ⅱ)抛物线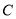 的方程为
的方程为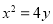 ,即
,即 ,求导得
,求导得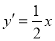 ..5分
..5分
设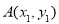 ,
,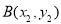 ,其中
,其中 ,
,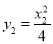 ,
,
则切线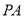 ,
,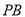 的斜率分别为
的斜率分别为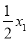 ,
, ,
,
所以切线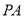 的方程为
的方程为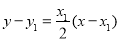 ,即
,即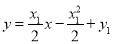 ,即
,即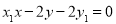 ,
,
同理可得切线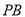 的方程为
的方程为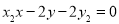 ..6分
..6分
因为切线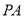 ,
,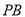 均过点
均过点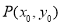 ,所以
,所以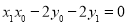 ,
,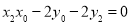 ,
,
所以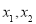 为方程
为方程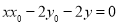 的两组解
的两组解
所以直线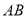 的方程为
的方程为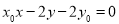 .8分
.8分
①当点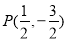 时,直线
时,直线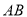 的方程为
的方程为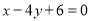 ; 9分
; 9分
②由抛物线定义知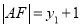 ,
,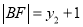
所以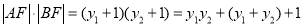
联立方程 消去
消去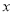 整理得
整理得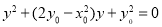 ,
,
故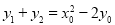 ,
,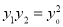 10分
10分
所以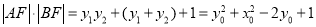
又因为点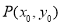 在直线
在直线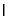 上,所以
上,所以 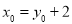
所以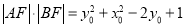

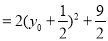
所以,当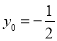 时,
时,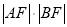 取得最小值,且最小值为
取得最小值,且最小值为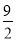 .12分
.12分
法二: (Ⅰ)设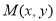 ,依题意:
,依题意: 
即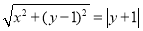
化简得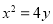
则轨迹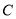 的方程为
的方程为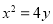 ..4分
..4分
(Ⅱ) ① 依题意过点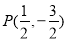 作曲线
作曲线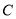 的切线,可知切线的斜率存在,设为
的切线,可知切线的斜率存在,设为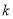 ,
,
则切线的方程为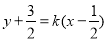 ,即
,即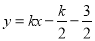 , ..5分
, ..5分
联立 消
消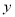 得:
得: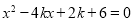 ①
①
由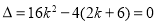 解得
解得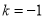 或
或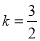
将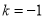 代入①式可得
代入①式可得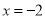 ,即
,即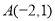
将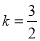 代入①式可得
代入①式可得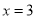 ,即
,即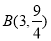
 直线
直线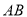 的方程为
的方程为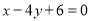 ; ..8分
; ..8分
②同法一 ..12分
考点:圆锥曲线及其在最值中的应用


科目:高中数学 来源:2014-2015学年江西省六校高三3月联考文科数学试卷(解析版) 题型:填空题
对于实数x,用[x]表示不超过x的最大整数,如[-0.5]=-1, [3, 2]=3,若n∈N*, an=[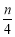 ], Sn为数列{an}的前n项和,则S8= ,S4n= .
], Sn为数列{an}的前n项和,则S8= ,S4n= .
查看答案和解析>>
科目:高中数学 来源:2014-2015学年福建省等高三上学期三校联考文科数学试卷(解析版) 题型:填空题
利用函数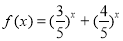
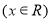 是减函数可以求方程
是减函数可以求方程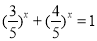 的解.
的解.
由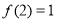 可知原方程有唯一解
可知原方程有唯一解 ,类比上述思路可知不等式
,类比上述思路可知不等式 的解集是 .
的解集是 .
查看答案和解析>>
科目:高中数学 来源:2014-2015学年福建省等高三上学期三校联考理科数学试卷(解析版) 题型:填空题
定义一个对应法则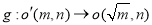
 ,现有点
,现有点 与
与 ,点
,点 是线段
是线段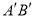 上一动点,按定义的对应法则
上一动点,按定义的对应法则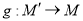 ,当点
,当点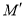 在线段
在线段 上从点的
上从点的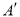 开始运动到点
开始运动到点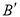 结束时,则点
结束时,则点 的对应点
的对应点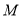 所形成的轨迹与x轴围成的面积为
所形成的轨迹与x轴围成的面积为
查看答案和解析>>
科目:高中数学 来源:2015年东北三省四市教研联合体高考模拟试卷(一)理科数学试卷(解析版) 题型:解答题
(本小题满分10分)选修4-1:几何证明选讲
如图, 为
为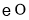 上的三个点,
上的三个点,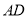 是
是 的平分线,交
的平分线,交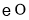 于点
于点 ,过
,过 作
作 的切线交
的切线交 的延长线于点
的延长线于点 .
.
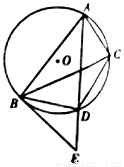
(1)证明: 平分
平分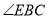 ;
;
(2)证明: .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com