
【题目】已知函数![]()
(1)若对任意的![]() ,
,![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(2)若![]() 的最小值为
的最小值为![]() ,求实数
,求实数![]() 的值;
的值;
(3)若对任意实数![]() 、
、![]() 、
、![]() ,均存在以
,均存在以![]() 、
、![]() 、
、![]() 为三边边长的三角形,求实数
为三边边长的三角形,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)问题等价于4x+k2x+1>0恒成立,分离出参数k后转化为求函数的最值问题即可;
(2)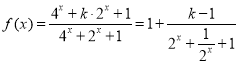 ,令
,令![]() ,则
,则![]() ,分k>1,k=1,k<1三种情况进行讨论求出f(x)的最小值,令其为﹣3即可解得k值;
,分k>1,k=1,k<1三种情况进行讨论求出f(x)的最小值,令其为﹣3即可解得k值;
(3)由题意得f(x1)+f(x2)>f(x3)对任意x1,x2,x3∈R恒成立,当k=1时易判断;当k>1,k<1时转化为函数的最值问题解决即可,借助(2)问结论易求函数的最值.
(1)因为4x+2x+1>0,所以f(x)>0恒成立,等价于4x+k2x+1>0恒成立,即k>﹣2x﹣2﹣x恒成立,
因为﹣2x﹣2﹣x=﹣(2x+2﹣x)≤﹣2,当且仅当2x=2﹣x,即x=0时取等号,所以k>﹣2.
(2)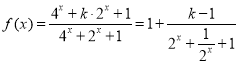 ,令
,令![]() ,则
,则![]() ,
,
当k>1时,![]() 无最小值,舍去;
无最小值,舍去;
当k=1时,y=1,最小值不是﹣3,舍去;
当k<1时,![]() ,最小值为
,最小值为![]() ,解得
,解得![]() .
.
综上所述,k=﹣11.
(3)由题意,f(x1)+f(x2)>f(x3)对任意x1,x2,x3∈R恒成立.
当k>1时,因![]() ,且
,且![]() ,故
,故![]() ,即1<k≤4;
,即1<k≤4;
当k=1时,f(x1)=f(x2)=f(x3)=1,满足条件;
当k<1时,![]() ,且
,且![]() ,故
,故![]() ,解得
,解得![]() ;
;
综上所述,![]()


科目:高中数学 来源: 题型:
【题目】已知曲线C1:y=cos x,C2:y=sin (2x+![]() ),则下面结论正确的是( )
),则下面结论正确的是( )
A. 把C1上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向右平移![]() 个单位长度,得到曲线C2
个单位长度,得到曲线C2
B. 把C1上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向左平移![]() 个单位长度,得到曲线C2
个单位长度,得到曲线C2
C. 把C1上各点的横坐标缩短到原来的![]() 倍,纵坐标不变,再把得到的曲线向右平移
倍,纵坐标不变,再把得到的曲线向右平移![]() 个单位长度,得到曲线C2
个单位长度,得到曲线C2
D. 把C1上各点的横坐标缩短到原来的![]() 倍,纵坐标不变,再把得到的曲线向左平移
倍,纵坐标不变,再把得到的曲线向左平移![]() 个单位长度,得到曲线C2
个单位长度,得到曲线C2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中真命题是( )
(1)在![]() 的二项式展开式中,共有
的二项式展开式中,共有![]() 项有理项;
项有理项;
(2)若事件![]() 、
、![]() 满足
满足![]() ,
,![]() ,
,![]() ,则事件
,则事件![]() 、
、![]() 是相互独立事件;
是相互独立事件;
(3)根据最近![]() 天某医院新增疑似病例数据,“总体均值为
天某医院新增疑似病例数据,“总体均值为![]() ,总体方差为
,总体方差为![]() ”,可以推测“最近
”,可以推测“最近![]() 天,该医院每天新增疑似病例不超过
天,该医院每天新增疑似病例不超过![]() 人”.
人”.
A.(1)(2)B.(1)(3)C.(2)(3)D.(1)(2)(3)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() 是非零实常数)满足
是非零实常数)满足![]() 且方程
且方程![]() 有且仅有一个实数解.
有且仅有一个实数解.
(1)求![]() 的值
的值
(2)当![]() 时,不等式
时,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围
的取值范围
(3)在直角坐标系中,求定点![]() 到函数
到函数![]() 图像上的任意一点
图像上的任意一点![]() 的距离
的距离![]() 的最小值,并求取得最小值时
的最小值,并求取得最小值时![]() 的值
的值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() (
(![]() 为参数),将曲线
为参数),将曲线![]() 上的所有点的横坐标保持不变,纵坐标缩短为原来的
上的所有点的横坐标保持不变,纵坐标缩短为原来的![]() 后得到曲线
后得到曲线![]() ;以坐标原点为极点,
;以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系,直线
轴的正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 和直线
和直线![]() 的直角坐标方程;
的直角坐标方程;
(2)已知![]() ,设直线
,设直线![]() 与曲线
与曲线![]() 交于不同的
交于不同的![]() 、
、![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以直角坐标系原点O为极点,x轴的正半轴为极轴.已知点P的直角坐标为![]() ,点M的极坐标为
,点M的极坐标为![]() ,若直线l过点P,且倾斜角为
,若直线l过点P,且倾斜角为![]() ,圆C以M点为圆心,4为半径.
,圆C以M点为圆心,4为半径.
![]() 求直线l和圆C的极坐标方程;
求直线l和圆C的极坐标方程;
![]() 直线l与x轴y轴分别交于A,B两点,Q为圆C上一动点,求
直线l与x轴y轴分别交于A,B两点,Q为圆C上一动点,求![]() 面积的最小值.
面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() 、
、![]() .经过点
.经过点![]() 且倾斜角为
且倾斜角为![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 、
、![]() 两点(其中点
两点(其中点![]() 在
在![]() 轴上方),
轴上方),![]() 的周长为8.
的周长为8.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)如图,把平面![]() 沿
沿![]() 轴折起来,使
轴折起来,使![]() 轴正半轴和
轴正半轴和![]() 轴确定的半平面,与
轴确定的半平面,与![]() 负半轴和
负半轴和![]() 轴所确定的半平面互相垂直.
轴所确定的半平面互相垂直.
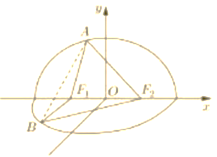
①若![]() ,求异面直线
,求异面直线![]() 和
和![]() 所成角的大小;
所成角的大小;
②若折叠后![]() 的周长为
的周长为![]() ,求
,求![]() 的大小.
的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】目前,中国有三分之二的城市面临“垃圾围城”的窘境. 我国的垃圾处理多采用填埋的方式,占用上万亩土地,并且严重污染环境. 垃圾分类把不易降解的物质分出来,减轻了土地的严重侵蚀,减少了土地流失. 2020年5月1日起,北京市将实行生活垃圾分类,分类标准为厨余垃圾、可回收物、有害垃圾和其它垃圾四类 .生活垃圾中有30%~40%可以回收利用,分出可回收垃圾既环保,又节约资源. 如:回收利用1吨废纸可再造出0.8吨好纸,可以挽救17棵大树,少用纯碱240千克,降低造纸的污染排放75%,节省造纸能源消耗40%~50%.
现调查了北京市5个小区12月份的生活垃圾投放情况,其中可回收物中废纸和塑料品的投放量如下表:
|
|
|
|
| |
废纸投放量(吨) | 5 | 5.1 | 5.2 | 4.8 | 4.9 |
塑料品投放量(吨) | 3.5 | 3.6 | 3.7 | 3.4 | 3.3 |
(Ⅰ)从![]() 这5个小区中任取1个小区,求该小区12月份的可回收物中,废纸投放量超过5吨且塑料品投放量超过3.5吨的概率;
这5个小区中任取1个小区,求该小区12月份的可回收物中,废纸投放量超过5吨且塑料品投放量超过3.5吨的概率;
(Ⅱ)从![]() 这5个小区中任取2个小区,记
这5个小区中任取2个小区,记![]() 为12月份投放的废纸可再造好纸超过4吨的小区个数,求
为12月份投放的废纸可再造好纸超过4吨的小区个数,求![]() 的分布列及期望.
的分布列及期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com