练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】下列命题中真命题是（ ）

    （1）在的二项式展开式中，共有项有理项；

    （2）若事件、满足，，，则事件、是相互独立事件；

    （3）根据最近天某医院新增疑似病例数据，“总体均值为，总体方差为”，可以推测“最近天，该医院每天新增疑似病例不超过人”.

    A.（1）（2）B.（1）（3）C.（2）（3）D.（1）（2）（3）

    【答案】D

    【解析】

    对三个命题分别判断真假，即可得出结论.

    对于（1），的二项展开式的通项为，

    当、、、时，为有理项，共有个有理项，故（1）正确；

    对于（2），事件、满足，，，

    所以，满足、为相互独立事件，故（2）正确；

    对于（3），当总体平均数是，若有一个数据超过，则方差就接近于，

    所以，总体均值为，总体方差为时，没有数据超过，故（3）正确.

    故选：D.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知函数f(x)＝A cos(ωx＋φ)(A＞0，ω＞0)的部分图象如图所示，下面结论错误的是(　　)

    A. 函数f(x)的最小正周期为

    B. 函数f(x)的图象可由g(x)＝Acos ωx的图象向右平移个单位长度得到

    C. 函数f(x)的图象关于直线x＝对称

    D. 函数f(x)在区间上单调递增

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知为实数，函数，且函数是偶函数，函数在区间上的减函数，且在区间上是增函数.

    （1）求函数的解析式；

    （2）求实数的值；

    （3）设，问是否存在实数，使得在区间上有最小值为？若存在，求出的值；若不存在，说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某快递公司在某市的货物转运中心，拟引进智能机器人分拣系统，以提高分拣效率和降低物流成本，已知购买x台机器人的总成本为万元．

    （1）若使每台机器人的平均成本最低，问应买多少台？

    （2）现按（1）中的数量购买机器人，需要安排m人将邮件放在机器人上，机器人将邮件送达指定落袋格口完成分拣（如图）．经实验知，每台机器人的日平均分拣量为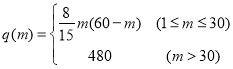，（单位：件）．已知传统的人工分拣每人每日的平均分拣量为1200件，问引进机器人后，日平均分拣量达最大时，用人数量比引进机器人前的用人数量最多可减少百分之几？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】2019年1月1日新修订的个税法正式实施，规定：公民全月工资、薪金所得不超过5000元的部分不必纳税，超过5000元的部分为全月应纳税所得额.此项税款按下表分段累计计算（预扣）：

    全月应缴纳所得额

    税率

    不超过3000元的部分

    超过3000元至12000元的部分

    超过12000元至25000元的部分

    国家在实施新个税时，考虑到纳税人的实际情况，实施了《个人所得税税前专项附加扣税暂行办法》，具体如下表：

    项目

    每月税前抵扣金额（元）

    说明

    子女教育

    1000

    一年按12月计算，可扣12000元

    继续教育

    400

    一年可扣除4800元，若是进行技能职业教育或者专业技术职业资格教育一年可扣除3600元

    大病医疗

    5000

    一年最高抵扣金额为60000元

    住房贷款利息

    1000

    一年可扣除12000元，若夫妻双方在同一城市工作，可以选择一方来扣除

    住房租金

    1500/1000/800

    扣除金额需要根据城市而定

    赡养老人

    2000

    一年可扣除24000元，若不是独生子女，子女平均扣除.赡养老人年龄需要在60周岁及以上

    老李本人为独生子女，家里有70岁的老人需要赡养，有一个女儿正读高三，他每月还需缴纳住房贷款2734元.若2019年11月老李工资，薪金所得为20000元，按照《个人所得税税前专项附加扣税暂行办法》，则老李应缴纳税款（预扣）为______元.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，矩形是一个历史文物展览厅的俯视图，点在上，在梯形区域内部展示文物，是玻璃幕墙，游客只能在区域内参观．在上点处安装一可旋转的监控摄像头．为监控角，其中、在线段（含端点）上，且点在点的右下方．经测量得知：米，米，米，．记(弧度)，监控摄像头的可视区域的面积为平方米．

    （1）求关于的函数关系式，并写出的取值范围；（参考数据：）

    （2）求的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆经过点，，点为椭圆的右顶点，直线与椭圆相交于不同于点的两个点、.

    （1）求椭圆的标准方程；

    （2）当时，求面积的最大值；

    （3）若，求证：为定值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数

    （1）若对任意的，恒成立，求实数的取值范围；

    （2）若的最小值为，求实数的值；

    （3）若对任意实数、、，均存在以、、为三边边长的三角形，求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】为了解某地区的“微信健步走”活动情况,现用分层抽样的方法从中抽取老、中、青三个年龄段人员进行问卷调查.已知抽取的样本同时满足以下三个条件:

    （i）老年人的人数多于中年人的人数;

    （ii）中年人的人数多于青年人的人数;

    （iii）青年人的人数的两倍多于老年人的人数.

    ①若青年人的人数为4,则中年人的人数的最大值为___________.

    ②抽取的总人数的最小值为__________．

    查看答案和解析>>

    同步练习册答案