
����Ŀ��ij��ݹ�˾��ij�еĻ���ת�����ģ����������ܻ����˷ּ�ϵͳ������߷ּ�Ч�ʺͽ��������ɱ�����֪����x̨�����˵��ܳɱ�Ϊ![]() ��Ԫ��
��Ԫ��

��1����ʹÿ̨�����˵�ƽ���ɱ���ͣ���Ӧ�����̨��
��2���ְ���1���е�������������ˣ���Ҫ����m�˽��ʼ����ڻ������ϣ������˽��ʼ��ʹ�ָ����������ɷּ���ͼ������ʵ��֪��ÿ̨�����˵���ƽ���ּ���Ϊ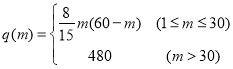 ������λ����������֪��ͳ���˹��ּ�ÿ��ÿ�յ�ƽ���ּ���Ϊ1200���������������˺���ƽ���ּ��������ʱ����������������������ǰ�������������ɼ��ٰٷ�֮����
������λ����������֪��ͳ���˹��ּ�ÿ��ÿ�յ�ƽ���ּ���Ϊ1200���������������˺���ƽ���ּ��������ʱ����������������������ǰ�������������ɼ��ٰٷ�֮����
���𰸡���1��300̨����2��![]() .
.
��������
��1�����ܳɱ�![]() ��Ԫ���ɵ�ÿ̨�����˵�ƽ���ɱ�
��Ԫ���ɵ�ÿ̨�����˵�ƽ���ɱ�![]() ��Ȼ�����û�������ʽ����ֵ��
��Ȼ�����û�������ʽ����ֵ��
��2�����������˺�ÿ̨�����˵���ƽ���ּ���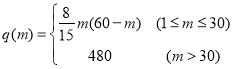 ���ֶ����300̨�����˵���ƽ���ּ��������ֵ�������������������ֵ����1200���ɵ÷ּ��������ֵʱ���贫ͳ�ּ���Ҫ��������𰸿���
���ֶ����300̨�����˵���ƽ���ּ��������ֵ�������������������ֵ����1200���ɵ÷ּ��������ֵʱ���贫ͳ�ּ���Ҫ��������𰸿���
�⣺��1�����ܳɱ�![]() ��Ԫ��
��Ԫ��
�ɵ�ÿ̨�����˵�ƽ���ɱ���
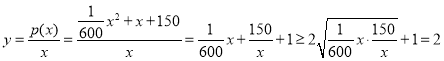 ��
��
���ҽ���![]() ����
����![]() ʱ����ʽ�Ⱥų�����
ʱ����ʽ�Ⱥų�����
����ʹÿ̨�����˵�ƽ���ɱ���ͣ�Ӧ��300̨��
��2�����������˺�ÿ̨�����˵���ƽ���ּ���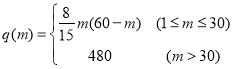 ��
��
��![]() ʱ��300̨�����˵���ƽ���ּ���Ϊ
ʱ��300̨�����˵���ƽ���ּ���Ϊ![]() ��
��
�൱![]() ʱ����ƽ���ּ��������ֵ144000��
ʱ����ƽ���ּ��������ֵ144000��
��![]() ʱ����ƽ���ּ���Ϊ480��300��144000��
ʱ����ƽ���ּ���Ϊ480��300��144000��
��300̨�����˵���ƽ���ּ��������ֵΪ144000����
����ͳ�˹��ּ�144000��������Ҫ����Ϊ![]() �ˣ�
�ˣ�
����ƽ���ּ��������ֵʱ����������������������ǰ�������������ɼ���![]() ��
��


 �ƸԺ���ȫ�����Ų��Ծ�ϵ�д�
�ƸԺ���ȫ�����Ų��Ծ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵxOy�У�����C�IJ�������Ϊ![]() ������Ϊ����������ԭ��Ϊ���㣬x��Ǹ�����Ϊ���Ὠ��������ϵ��
������Ϊ����������ԭ��Ϊ���㣬x��Ǹ�����Ϊ���Ὠ��������ϵ��
��1��������C�ļ����귽�̣�
��2����ƽ��ֱ������ϵxOy�У�A����2��0����B��0����2����M������C������һ�㣬����ABM�������Сֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��2019��1��3���϶��ĺ�̽�����ɹ�ʵ��������ʷ���״�����������½���ҹ�������ҵȡ����һ�ش�ɾͣ�ʵ������������½��Ҫ�����һ���ؼ����������ǵ�����̽������ͨѶ��ϵ��Ϊ���������⣬�������϶��ĺ��м��ǡ�ȵ�š���ȵ������Χ�Ƶ�����������![]() ��Ĺ�����У�
��Ĺ�����У�![]() ����ƽ��㣬λ�ڵ������ߵ��ӳ����ϣ����������ΪM������������ΪM�������¾���ΪR��
����ƽ��㣬λ�ڵ������ߵ��ӳ����ϣ����������ΪM������������ΪM�������¾���ΪR��![]() �㵽����ľ���Ϊr������ţ���˶����ɺ������������ɣ�r���㷽�̣�
�㵽����ľ���Ϊr������ţ���˶����ɺ������������ɣ�r���㷽�̣�
![]() .
.
��![]() ������
������![]() ��ֵ��С������ڽ��Ƽ�����
��ֵ��С������ڽ��Ƽ�����![]() ����r�Ľ���ֵΪ
����r�Ľ���ֵΪ
A.  B.
B. 
C.  D.
D. 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijý��Ϊ����ϲ�����ֽ�Ŀ![]() �Ƿ�������Ա��йأ������ȡ��30�����Ժ�30��Ů�Թ��ڣ�������õȸ�����ͼ��ʾ��ͼ��
�Ƿ�������Ա��йأ������ȡ��30�����Ժ�30��Ů�Թ��ڣ�������õȸ�����ͼ��ʾ��ͼ��
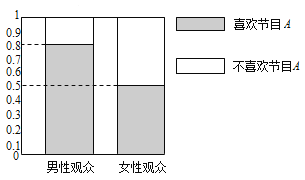
��1�����ݸõȸ�����ͼ���������![]() �����������ö����Լ���ķ����������ܷ��ڷ�����ĸ��ʲ�����0.05��ǰ������Ϊϲ�����ֽ�Ŀ
�����������ö����Լ���ķ����������ܷ��ڷ�����ĸ��ʲ�����0.05��ǰ������Ϊϲ�����ֽ�Ŀ![]() ������Ա��йأ�
������Ա��йأ�

��2�����Թ����а�ϲ����Ŀ![]() ����÷ֲ�����ķ�����ȡ5������һ�����飮����5������ѡ2������ǡ��1��ϲ����Ŀ
����÷ֲ�����ķ�����ȡ5������һ�����飮����5������ѡ2������ǡ��1��ϲ����Ŀ![]() ��1����ϲ����Ŀ
��1����ϲ����Ŀ![]() �ĸ��ʣ�
�ĸ��ʣ�
����
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
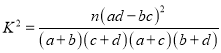 ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������R�ϵĺ���![]() ����ͼ�����������ϵģ��Ҵ��ڳ���
����ͼ�����������ϵģ��Ҵ��ڳ���![]() ʹ��
ʹ��![]() ������ʵ��x�����������
������ʵ��x�����������![]() ��һ����k�������������������н�������ȷ�������Ϊ____________.
��һ����k�������������������н�������ȷ�������Ϊ____________.
��![]() ��һ����k����������������
��һ����k����������������![]() ���ǡ�k��������������
���ǡ�k��������������
��![]() �dz���������Ψһ�ġ�k���������������ܡ�
�dz���������Ψһ�ġ�k���������������ܡ�![]() ������������������һ����㣻
������������������һ����㣻
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����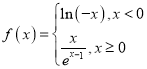 ��������
��������![]() ���ĸ����ȵ�ʵ��������
���ĸ����ȵ�ʵ��������![]() ��ȡֵ��Χ�ǣ� ��
��ȡֵ��Χ�ǣ� ��
A.![]() B.
B.![]() ��
��![]()
C.![]() ��
��![]() D.
D.![]() ��
��![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ������ϵ![]() �У�����
�У�����![]() �IJ�������Ϊ
�IJ�������Ϊ![]() ��
��![]() ��������
Ϊ��������![]() Ϊ
Ϊ![]() �ϵĶ��㣬
�ϵĶ��㣬![]() ������
������![]() ����
����![]() �Ĺ켣Ϊ����
�Ĺ켣Ϊ����![]() ��
��
��1��������![]() ��ֱ�����귽�̣�
��ֱ�����귽�̣�
��2������Ϊ![]() ���㣬
���㣬![]() ���������Ϊ����ļ�����ϵ�У�����
���������Ϊ����ļ�����ϵ�У�����![]() ��
��![]() �����ڼ���Ľ���Ϊ
�����ڼ���Ľ���Ϊ![]() ����
����![]() �����ڼ���Ľ���Ϊ
�����ڼ���Ľ���Ϊ![]() ����
����![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��![]() ��
��![]() ���DZ߳�Ϊ2���������Σ�ƽ��
���DZ߳�Ϊ2���������Σ�ƽ��![]() ƽ��
ƽ��![]() ��
��![]() ƽ��
ƽ��![]() ��
��![]() .
.
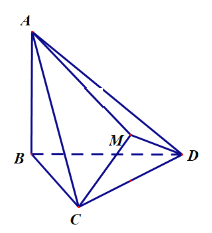
��1��֤����ֱ��![]() ƽ��
ƽ��![]()
��2����ֱ��![]() ��ƽ��
��ƽ��![]() ���ɵĽǵĴ�С��
���ɵĽǵĴ�С��
��3����ƽ��![]() ��ƽ��
��ƽ��![]() ���ɵĶ���ǵ�����ֵ.
���ɵĶ���ǵ�����ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪������![]() ��ƽ��
��ƽ��![]() ƽ��
ƽ��![]() ,
,![]() ��
��![]() �ֱ���
�ֱ���![]() ���е�.
���е�.

��1��֤����![]() ��
��
��2����ֱ��![]() ��ƽ��
��ƽ��![]() ���ɽǵ�����ֵ.
���ɽǵ�����ֵ.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com