
【题目】如图,![]() 与
与![]() 都是边长为2的正三角形,平面
都是边长为2的正三角形,平面![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() .
.
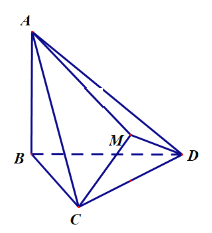
(1)证明:直线![]() 平面
平面![]()
(2)求直线![]() 与平面
与平面![]() 所成的角的大小;
所成的角的大小;
(3)求平面![]() 与平面
与平面![]() 所成的二面角的正弦值.
所成的二面角的正弦值.
【答案】(1)证明见解析;(2) ![]() .(3)
.(3) ![]()
【解析】
(1)取CD中点O,连接MO,由面面垂直的性质定理得到线面垂直,再由线面平行的判定定理即证明MO![]() AB,得到线面平行;
AB,得到线面平行;
(2)取![]() 中点
中点![]() ,连
,连![]() ,
,![]() ,以
,以![]() 为原点,直线
为原点,直线![]() 、
、![]() 、
、![]() 为
为![]() 轴,
轴,![]() 轴,
轴,![]() 轴,建立空间直角坐标系,从而得到
轴,建立空间直角坐标系,从而得到![]() 与平面
与平面![]() 的法向量
的法向量![]() 的坐标,再求线面角的正弦值,从而得到线面角的大小;
的坐标,再求线面角的正弦值,从而得到线面角的大小;
(3)分别求出两个面的法向量,再求法向量夹角的余弦值,进而得到二面角的余弦值,最后利用同角三角函数的基本关系得到二面角的正弦值.
(1)取CD中点O,连接MO,平面![]() 平面
平面![]() ,则
,则![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,所以MO
,所以MO![]() AB.
AB.
又![]() 面MCD,
面MCD,![]() 面MCD,所以
面MCD,所以![]() 面MCD.
面MCD.
(2)取![]() 中点
中点![]() ,连
,连![]() ,
,![]() ,则
,则![]() ,
,![]() ,
,
又平面![]() 平面
平面![]() ,则
,则![]() 平面
平面![]() .
.
以![]() 为原点,直线
为原点,直线![]() 、
、![]() 、
、![]() 为
为![]() 轴,
轴,![]() 轴,
轴,![]() 轴,建立空间直角坐标系如图.
轴,建立空间直角坐标系如图.
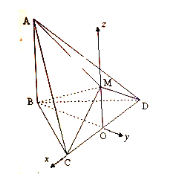
![]() ,则各点坐标分别为
,则各点坐标分别为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
设直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,
,
因为![]() ,平面
,平面![]() 的法向量为
的法向量为![]() ,
,
则有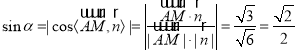 ,所以
,所以![]() .
.
(3)![]() ,
,![]() .设平面
.设平面![]() 的法向量为
的法向量为![]() ,
,
由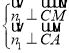 得
得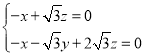 .解得
.解得![]() ,
,![]() ,取
,取![]() ,
,
又平面![]() 的法向量为
的法向量为![]() ,则
,则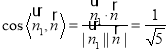
设所求二面角为![]() ,则
,则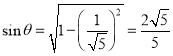 .
.


科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左右焦点分别为
的左右焦点分别为![]() ,
,![]() ,点
,点![]() ,
,![]() 是椭圆
是椭圆![]() 的左右顶点,点
的左右顶点,点![]() 是椭圆
是椭圆![]() 上一动点,
上一动点,![]() 的周长为6,且直线
的周长为6,且直线![]() ,
,![]() 的斜率之积为
的斜率之积为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)若![]() 、
、![]() 为椭圆
为椭圆![]() 上位于
上位于![]() 轴同侧的两点,且
轴同侧的两点,且![]() ,求四边形
,求四边形![]() 面积的取值范围.
面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某快递公司在某市的货物转运中心,拟引进智能机器人分拣系统,以提高分拣效率和降低物流成本,已知购买x台机器人的总成本为![]() 万元.
万元.

(1)若使每台机器人的平均成本最低,问应买多少台?
(2)现按(1)中的数量购买机器人,需要安排m人将邮件放在机器人上,机器人将邮件送达指定落袋格口完成分拣(如图).经实验知,每台机器人的日平均分拣量为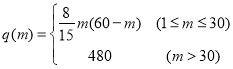 ,(单位:件).已知传统的人工分拣每人每日的平均分拣量为1200件,问引进机器人后,日平均分拣量达最大时,用人数量比引进机器人前的用人数量最多可减少百分之几?
,(单位:件).已知传统的人工分拣每人每日的平均分拣量为1200件,问引进机器人后,日平均分拣量达最大时,用人数量比引进机器人前的用人数量最多可减少百分之几?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,圆
中,圆![]() 的参数方程为
的参数方程为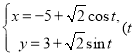 为参数),在以原点
为参数),在以原点![]() 为极点,
为极点,![]() 轴的非负半轴为极轴建立的极坐标系中,直线
轴的非负半轴为极轴建立的极坐标系中,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求圆![]() 的普通方程和直线
的普通方程和直线![]() 的直角坐标方程;
的直角坐标方程;
(2)设直线![]() 与
与![]() 轴,
轴,![]() 轴分别交于
轴分别交于![]() 两点,点
两点,点![]() 是圆
是圆![]() 上任一点,求
上任一点,求![]() 面积的最小值.
面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂利用随机数表对生产的600个零件进行抽样测试,先将600个零件进行编号,编号分别为001,002,![]() ,599,600从中抽取60个样本,如下提供随机数表的第4行到第6行:
,599,600从中抽取60个样本,如下提供随机数表的第4行到第6行:
32 21 18 34 29 78 64 54 07 32 52 42 06 44 38 12 23 43 56 77 35 78 90 56 42
84 42 12 53 31 34 57 86 07 36 25 30 07 32 86 23 45 78 89 07 23 68 96 08 04
32 56 78 08 43 67 89 53 55 77 34 89 94 83 75 22 53 55 78 32 45 77 89 23 45
若从表中第6行第6列开始向右依次读取3个数据,则得到的第6个样本编号![]()
![]()
A. 522B. 324C. 535D. 578
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com