
【题目】如图,矩形![]() 是一个历史文物展览厅的俯视图,点
是一个历史文物展览厅的俯视图,点![]() 在
在![]() 上,在梯形
上,在梯形![]() 区域内部展示文物,
区域内部展示文物,![]() 是玻璃幕墙,游客只能在
是玻璃幕墙,游客只能在![]() 区域内参观.在
区域内参观.在![]() 上点
上点![]() 处安装一可旋转的监控摄像头.
处安装一可旋转的监控摄像头.![]() 为监控角,其中
为监控角,其中![]() 、
、![]() 在线段
在线段![]() (含端点)上,且点
(含端点)上,且点![]() 在点
在点![]() 的右下方.经测量得知:
的右下方.经测量得知:![]() 米,
米,![]() 米,
米,![]() 米,
米,![]() .记
.记![]() (弧度),监控摄像头的可视区域
(弧度),监控摄像头的可视区域![]() 的面积为
的面积为![]() 平方米.
平方米.

(1)求![]() 关于
关于![]() 的函数关系式,并写出
的函数关系式,并写出![]() 的取值范围;(参考数据:
的取值范围;(参考数据:![]() )
)
(2)求![]() 的最小值.
的最小值.
 寒假学与练系列答案
寒假学与练系列答案科目:高中数学 来源: 题型:
【题目】某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费![]() (单位:万元)对年销售量
(单位:万元)对年销售量![]() (单位:吨)和年利润
(单位:吨)和年利润![]() (单位:万元)的影响.对近六年的年宣传费
(单位:万元)的影响.对近六年的年宣传费![]() 和年销售量
和年销售量![]() 的数据作了初步统计,得到如下数据:
的数据作了初步统计,得到如下数据:
年份 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 |
年宣传费 | 38 | 48 | 58 | 68 | 78 | 88 |
年销售量 | 16.8 | 18.8 | 20.7 | 22.4 | 24.0 | 25.5 |
经电脑模拟,发现年宣传费![]() (万元)与年销售量
(万元)与年销售量![]() (吨)之间近似满足关系式
(吨)之间近似满足关系式![]() ,即
,即![]() .对上述数据作了初步处理,得到相关的值如下表:
.对上述数据作了初步处理,得到相关的值如下表:
|
|
|
|
75.3 | 24.6 | 18.3 | 101.4 |
(1)根据所给数据,求![]() 关于
关于![]() 的回归方程;
的回归方程;
(2)规定当产品的年销售量![]() (吨)与年宣传费
(吨)与年宣传费![]() (万元)的比值在区间
(万元)的比值在区间![]() 内时认为该年效益良好.该公司某
内时认为该年效益良好.该公司某![]() 年投入的宣传费用(单位:万元)分别为:
年投入的宣传费用(单位:万元)分别为:![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,试根据回归方程估计年销售量,从这
,试根据回归方程估计年销售量,从这![]() 年中任选
年中任选![]() 年,记其中选到效益良好年的数量为
年,记其中选到效益良好年的数量为![]() ,试求随机变量
,试求随机变量![]() 的分布列和期望.(其中
的分布列和期望.(其中![]() 为自然对数的底数,
为自然对数的底数,![]() )
)
附:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线
,其回归直线![]() 中的斜率和截距的最小二乘估计分别为
中的斜率和截距的最小二乘估计分别为 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国某沙漠,曾被称为“死亡之海”,截止2018年年底该地区的绿化率只有![]() ,计划从2019年开始使用无人机飞播造林,弹射的种子可以直接打入沙面里头,实现快速播种,每年原来沙漠面积的
,计划从2019年开始使用无人机飞播造林,弹射的种子可以直接打入沙面里头,实现快速播种,每年原来沙漠面积的![]() 将被改为绿洲,但同时原有绿洲面积的
将被改为绿洲,但同时原有绿洲面积的![]() 还会被沙漠化。设该地区的面积为
还会被沙漠化。设该地区的面积为![]() ,2018年年底绿洲面积为
,2018年年底绿洲面积为![]() ,经过一年绿洲面积为
,经过一年绿洲面积为![]() ……经过
……经过![]() 年绿洲面积为
年绿洲面积为![]() ,
,
(1)求经过![]() 年绿洲面积
年绿洲面积![]() ;
;
(2)截止到哪一年年底,才能使该地区绿洲面积超过![]() ?(取
?(取![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,△ABC和△BCD所在平面互相垂直,且AB=BC=BD=2.∠ABC=∠DBC=120°,E、F分别为AC、DC的中点. 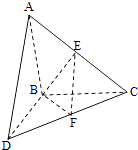
(1)求证:EF⊥BC;
(2)求二面角E﹣BF﹣C的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某湿地公园内有一条河,现打算建一座桥将河两岸的路连接起来,剖面设计图纸如下:

其中,点![]() 为
为![]() 轴上关于原点对称的两点,曲线段
轴上关于原点对称的两点,曲线段![]() 是桥的主体,
是桥的主体,![]() 为桥顶,且曲线段
为桥顶,且曲线段![]() 在图纸上的图形对应函数的解析式为
在图纸上的图形对应函数的解析式为![]() ,曲线段
,曲线段![]() 均为开口向上的抛物线段,且
均为开口向上的抛物线段,且![]() 分别为两抛物线的顶点,设计时要求:保持两曲线在各衔接处(
分别为两抛物线的顶点,设计时要求:保持两曲线在各衔接处(![]() )的切线的斜率相等.
)的切线的斜率相等.
(1)求曲线段![]() 在图纸上对应函数的解析式,并写出定义域;
在图纸上对应函数的解析式,并写出定义域;
(2)车辆从![]() 经
经![]() 倒
倒![]() 爬坡,定义车辆上桥过程中某点
爬坡,定义车辆上桥过程中某点![]() 所需要的爬坡能力为:
所需要的爬坡能力为:![]() (该点
(该点![]() 与桥顶间的水平距离)
与桥顶间的水平距离)![]() (设计图纸上该点处的切线的斜率),其中
(设计图纸上该点处的切线的斜率),其中![]() 的单位:米.若该景区可提供三种类型的观光车:①游客踏乘;②蓄电池动力;③内燃机动力.它们的爬坡能力分别为
的单位:米.若该景区可提供三种类型的观光车:①游客踏乘;②蓄电池动力;③内燃机动力.它们的爬坡能力分别为![]() 米,
米,![]() 米,
米,![]() 米,又已知图纸上一个单位长度表示实际长度
米,又已知图纸上一个单位长度表示实际长度![]() 米,试问三种类型的观光车是否都可以顺利过桥?
米,试问三种类型的观光车是否都可以顺利过桥?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数![]() 的一段图象过点
的一段图象过点![]() ,如图所示.
,如图所示.
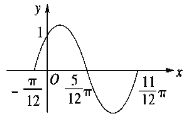
(1)求函数![]() 的表达式;
的表达式;
(2)将函数![]() 的图象向右平移
的图象向右平移![]() 个单位,得函数
个单位,得函数![]() 的图象,求
的图象,求![]() 的最大值,并求出此时自变量
的最大值,并求出此时自变量![]() 的集合,并写出该函数的增区间.
的集合,并写出该函数的增区间.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com