【题目】如图，在直三棱柱
中，
，
,
分别是
,
的中点．
（1）求证：
∥平面
；
（2）求证：平面
平面
．
【答案】（Ⅰ）详见解析（Ⅱ）详见解析
【解析】
试题分析：（Ⅰ）证明线面平行，一般利用线面平行判定定理，即从线线平行出发给予证明，而线线平行的寻找与论证，往往需要结合平几知识，如三角形中位线性质，及利用柱体性质，如上下底面对应边相互平行（Ⅱ）证明面面垂直，一般利用面面垂直判定定理，即从线面垂直出发给予证明，而线面垂直的证明，往往需要利用线面垂直判定与性质定理进行多次转化：由直棱柱性质得侧棱垂直于底面：
底面
，再转化为线线垂直
；又根据线线平行
，将线线垂直
进行转化
，再根据线面垂直判定定理得
平面
试题解析：证明：（1）因为
,
分别是
,
的中点，所以， ...........2分
又因为在三棱柱
中，
，所以
. ...............4分
又
平面
，
平面，所以
∥平面. ...............6分
（2）在直三棱柱中，
，
又
底面，所以. .............8分
又，，所以， ..........10分
又
平面，且
，所以平面. ...............12分
又
平面
，所以平面
平面
． ............14分
（注：第（2）小题也可以用面面垂直的性质定理证明平面，类似给分）
科目：高中数学 来源： 题型：
【题目】△ABC的内角A，B，C所对应的边分别为a，b，c．
（1）若a，b，c成等差数列，证明：sinA+sinC=2sin（A+C）；
（2）若a，b，c成等比数列，求cosB的最小值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设 
， 
， 
是非零向量，已知命题p：若 =0， =0，则 =0；命题q：若 ∥ ， ∥ ，则 ∥ ，则下列命题中真命题是（ ）
A.p∨q
B.p∧q
C.（￢p）∧（￢q）
D.p∨（￢q）
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某险种的基本保费为a(单位：元)，继续购买该险种的投保人称为续保人，续保人本年度的保费与其上年度出险次数的关联如下：
上年度出险次数 | 0 | 1 | 2 | 3 | 4 | ≥5 |
保费 | 0.85a | a | 1.25a | 1.5a | 1.75a | 2a |
随机调查了该险种的200名续保人在一年内的出险情况，得到如下统计表：
出险次数 | 0 | 1 | 2 | 3 | 4 | ≥5 |
频数 | 60 | 50 | 30 | 30 | 20 | 10 |
(1)记A为事件：“一续保人本年度的保费不高于基本保费”，求P(A)的估计值；
(2)记B为事件：“一续保人本年度的保费高于基本保费但不高于基本保费的160%”，求P(B)的估计值；
(3)求续保人本年度平均保费的估计值．
查看答案和解析>>
科目：高中数学 来源： 题型：
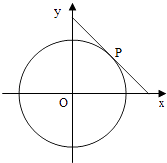
【题目】圆x2+y2=4的切线与x轴正半轴，y轴正半轴围成一个三角形，当该三角形面积最小时，切点为P（如图），双曲线C1： 
过点P且离心率为 
． 
（1）求C1的方程；
（2）若椭圆C2过点P且与C1有相同的焦点，直线l过C2的右焦点且与C2交于A，B两点，若以线段AB为直径的圆过点P，求l的方程．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，矩形
是一个历史文物展览厅的俯视图，点
在
上，在梯形
区域内部展示文物，
是玻璃幕墙，游客只能在
区域内参观．在
上点
处安装一可旋转的监控摄像头．
为监控角，其中
、
在线段（含端点）上，且点在点的右下方．经测量得知：
米，
米，
米，
．记
(弧度)，监控摄像头的可视区域
的面积为
平方米．
（1）求关于
的函数关系式，并写出的取值范围；（参考数据：
）
（2）求的最小值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某校高三年级共有学生
名，为了解学生某次月考的情况，抽取了部分学生的成绩（得分均为整数，满分为
分）进行统计，绘制出如下尚未完成的频率分布表：
分组 | 频数 | 频率 |
|
|
|
|
| |
|
| |
|
| |
| ||
|
|
（1）补充完整题中的频率分布表；
（2）若成绩在
为优秀，估计该校高三年级学生在这次月考中，成绩优秀的学生约为多少人.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】为了了解一片经济林的生长情况，随机抽测了其中60株树木的底部周长（单位：cm），所得数据均在区间[80，130]上，其频率分布直方图如图所示，则在抽测的60株树木中，有株树木的底部周长小于100cm．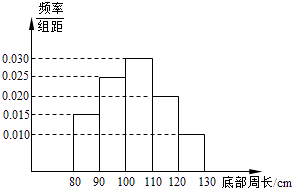 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
