
����Ŀ��ij��˾Ϊȷ����һ���Ͷ��ij�ֲ�Ʒ�������ѣ����˽���������![]() ����λ����Ԫ������������
����λ����Ԫ������������![]() ����λ���֣���������
����λ���֣���������![]() ����λ����Ԫ����Ӱ��.�Խ��������������
����λ����Ԫ����Ӱ��.�Խ��������������![]() ����������
����������![]() ���������˳���ͳ�ƣ��õ��������ݣ�
���������˳���ͳ�ƣ��õ��������ݣ�
��� | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 |
�������� | 38 | 48 | 58 | 68 | 78 | 88 |
�������� | 16.8 | 18.8 | 20.7 | 22.4 | 24.0 | 25.5 |
������ģ�⣬������������![]() ����Ԫ������������
����Ԫ������������![]() ���֣�֮����������ϵʽ
���֣�֮����������ϵʽ![]() ����
����![]() .�������������˳����������õ���ص�ֵ���±���
.�������������˳����������õ���ص�ֵ���±���
|
|
|
|
75.3 | 24.6 | 18.3 | 101.4 |
��1�������������ݣ���![]() ����
����![]() �Ļع鷽�̣�
�Ļع鷽�̣�
��2���涨����Ʒ����������![]() ���֣�����������
���֣�����������![]() ����Ԫ���ı�ֵ������
����Ԫ���ı�ֵ������![]() ��ʱ��Ϊ����Ч������.�ù�˾ij
��ʱ��Ϊ����Ч������.�ù�˾ij![]() ��Ͷ����������ã���λ����Ԫ���ֱ�Ϊ��
��Ͷ����������ã���λ����Ԫ���ֱ�Ϊ��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ���Ը��ݻع鷽�̹�����������������
���Ը��ݻع鷽�̹�����������������![]() ������ѡ
������ѡ![]() �꣬������ѡ��Ч�������������Ϊ
�꣬������ѡ��Ч�������������Ϊ![]() �������������
�������������![]() �ķֲ��к�����.������
�ķֲ��к�����.������![]() Ϊ��Ȼ�����ĵ�����
Ϊ��Ȼ�����ĵ�����![]() ��
��
��������һ������![]() ��
��![]() ������
������![]() ����ع�ֱ��
����ع�ֱ��![]() �е�б�ʺͽؾ����С���˹��Ʒֱ�Ϊ
�е�б�ʺͽؾ����С���˹��Ʒֱ�Ϊ ��
��![]() .
.
���𰸡���1��![]() ��2��������
��2��������
����������������1�������⣬��![]() ��
��![]() ��������Իع鷽�̼��㹫ʽ�ɵ����е����Իع鷽��Ϊ
��������Իع鷽�̼��㹫ʽ�ɵ����е����Իع鷽��Ϊ![]() .
.
��2��������ɵã�![]() ��������������Ч������������
��������������Ч������������![]() ���ɳ����ηֲ��ɵ���ֲ��У�������ѧ����Ϊ
���ɳ����ηֲ��ɵ���ֲ��У�������ѧ����Ϊ![]() .
.
��⣺��1����![]() ��
��![]() ����ȡ������
����ȡ������![]() ����
����![]() ��
��![]()
��![]() ����������ݣ��ã�
����������ݣ��ã�![]() ��
��![]() ��
��
![]() ��
��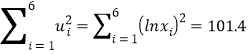 ��������
��������
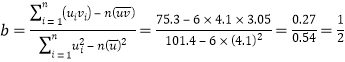 ��
��
![]() ����
����![]() ��
��
������ع鷽��Ϊ![]() .
.
��2����![]() ������
������![]() ����
����![]() ��������������������������
��������������������������
![]() �������
�������![]() ��
��![]() ��
��
![]() ��
��![]()
����![]() �ķֲ��������ʾ��
�ķֲ��������ʾ��
| 0 | 1 | 2 | 3 |
|
|
|
|
|
��![]() .
.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=cosx��sinx+cosx����![]() ��
��
��1����0������![]() �� ��sin��=
�� ��sin��=![]() �� ��f��������ֵ��
�� ��f��������ֵ��
��2������f��x������С�����ڼ������������䣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���躯��f��x��=ax2+lnx��
����a=��1ʱ������y=f��x����ͼ���ڵ㣨1��f��1�����������߷��̣�
������֪a��0��������y=f��x����ͼ������ֱ��y=-![]() ���·�����a��ȡֵ��Χ��
���·�����a��ȡֵ��Χ��
����f�䣨x��Ϊ����f��x���ĵ���������a=1�����ʣ�������[1��10]���Ƿ����k��k��100��������x1 �� x2 �� x3��xk �� ʹ��f�䣨x1��+f�䣨x2��+f�䣨x3��+��+f�䣨xk����2012��������֤����Ľ��ۣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����![]() ������
������![]() ������
������![]() .
.
��1������![]() �ĵ����ԣ�
�ĵ����ԣ�
��2����![]() ʱ������ʽ
ʱ������ʽ![]() ���������
���������![]() ����Сֵ.
����Сֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ABC���ڽ�A��B��C����Ӧ�ı߷ֱ�Ϊa��b��c��
��1����a��b��c�ɵȲ����У�֤����sinA+sinC=2sin��A+C����
��2����a��b��c�ɵȱ����У���cosB����Сֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������C���ϰ���ԲC1�� ![]() =1��a��b��0��y��0���Ͳ���������C2��y=��x2+1��y��0�����Ӷ��ɣ�C1��C2�Ĺ�����ΪA��B������C1��������Ϊ
=1��a��b��0��y��0���Ͳ���������C2��y=��x2+1��y��0�����Ӷ��ɣ�C1��C2�Ĺ�����ΪA��B������C1��������Ϊ ![]() ��
�� 
��1����a��b��ֵ��
��2������B��ֱ��l��C1 �� C2�ֱ��ڵ�P��Q�������ڵ�A��B������AP��AQ����ֱ��l�ķ��̣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪![]() ��
��![]() ����f��x��=
����f��x��=![]()
![]() ��
��
��1������f��x���Ľ���ʽ����С�����ڼ������������䣮
��2����![]() ʱ��f��x������Сֵ��-4�����ʱ����f��x�������ֵ���������Ӧ��x��ֵ��
ʱ��f��x������Сֵ��-4�����ʱ����f��x�������ֵ���������Ӧ��x��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����мס���������Ŀ���Լ���ĿÿͶ��10��Ԫ��һ���������1.2��Ԫ��1.18��Ԫ��1.17��Ԫ�ĸ��ʷֱ�Ϊ![]() ����֪����Ŀ���������Ʒ�۸�ĵ����йأ���ÿ�ε����У��۸��½��ĸ��ʶ���p(0<p<1)��������Ŀ��Ʒ�۸���һ���ڽ������ζ����ĵ���.������Ŀ��Ʒ�۸���һ���ڵ��½�����ΪX��������ĿÿͶ��10��Ԫ��Xȡ0��1��2ʱ��һ�����Ӧ������1.3��Ԫ��1.25��Ԫ��0.2��Ԫ.�������X1��X2�ֱ��ʾ�Լס�������Ŀ��Ͷ��10��Ԫһ��������.
����֪����Ŀ���������Ʒ�۸�ĵ����йأ���ÿ�ε����У��۸��½��ĸ��ʶ���p(0<p<1)��������Ŀ��Ʒ�۸���һ���ڽ������ζ����ĵ���.������Ŀ��Ʒ�۸���һ���ڵ��½�����ΪX��������ĿÿͶ��10��Ԫ��Xȡ0��1��2ʱ��һ�����Ӧ������1.3��Ԫ��1.25��Ԫ��0.2��Ԫ.�������X1��X2�ֱ��ʾ�Լס�������Ŀ��Ͷ��10��Ԫһ��������.
(1)��X1��X2�ĸ��ʷֲ��;�ֵE(X1)��E(X2)��
(2)��E(X1)<E(X2)ʱ����p��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������![]() ��һ����ʷ����չ�����ĸ���ͼ����
��һ����ʷ����չ�����ĸ���ͼ����![]() ��
��![]() �ϣ�������
�ϣ�������![]() �����ڲ�չʾ���
�����ڲ�չʾ���![]() �Dz���Ļǽ���ο�ֻ����
�Dz���Ļǽ���ο�ֻ����![]() �����ڲιۣ���
�����ڲιۣ���![]() �ϵ�
�ϵ�![]() ����װһ����ת�ļ������ͷ��
����װһ����ת�ļ������ͷ��![]() Ϊ��ؽǣ�����
Ϊ��ؽǣ�����![]() ��
��![]() ���߶�
���߶�![]() �����˵㣩�ϣ��ҵ�
�����˵㣩�ϣ��ҵ�![]() �ڵ�
�ڵ�![]() �����·�����������֪��
�����·�����������֪��![]() �ף�
�ף�![]() �ף�
�ף�![]() �ף�
�ף�![]() ����
����![]() (����)���������ͷ�Ŀ�������
(����)���������ͷ�Ŀ�������![]() �����Ϊ
�����Ϊ![]() ƽ���ף�
ƽ���ף�

��1����![]() ����
����![]() �ĺ�����ϵʽ����д��
�ĺ�����ϵʽ����д��![]() ��ȡֵ��Χ�����ο����ݣ�
��ȡֵ��Χ�����ο����ݣ�![]() ��
��
��2����![]() ����Сֵ��
����Сֵ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com