
【题目】在![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 在边
在边![]() 上,点
上,点![]() 关于直线
关于直线![]() 的对称点分别为
的对称点分别为![]() ,则
,则![]() 的面积的最大值为
的面积的最大值为
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】D
【解析】
解三角形,建立坐标系,设AD斜率为k,用k表示出B′纵坐标,代入面积公式得出面积关于k的函数,根据k的范围和函数单调性求出面积最大值.
由余弦定理可得AC2=AB2+BC2﹣2ABBCcosB=12+9﹣2×2![]() 3
3![]() 3,
3,
∴AC![]() ,且AC2+BC2=AB2,
,且AC2+BC2=AB2,
∴AC⊥BC,
以C为原点,以CB,CA为坐标轴建立平面直角坐标系,如图所示:
设直线AD的方程为y=kx![]() ,
,
当D与线段AB的端点重合时,B,B',C'在同一条直线上,不符合题意,
∴则k![]() ,设B′(m,n),显然n<0,
,设B′(m,n),显然n<0,
则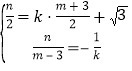 ,解得n
,解得n![]() ,
,
∵CC′∥BB′,
∴S△BB′C′=S△BB′C![]() ,
,
令f(k)![]() (k
(k![]() ),则f′(k)
),则f′(k)![]() ,
,
令f′(k)=0可得k![]() 或k
或k![]() (舍),
(舍),
∴当k![]() 时,f′(k)>0,当
时,f′(k)>0,当![]() k
k![]() 时,f′(k)<0,
时,f′(k)<0,
∴当k![]() 时,f(k)取得最大值f(
时,f(k)取得最大值f(![]() )
)![]() .
.
故选:D.


 步步高达标卷系列答案
步步高达标卷系列答案科目:高中数学 来源: 题型:
【题目】某地区某农产品近几年的产量统计如表:
年份 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 |
年份代码t | 1 | 2 | 3 | 4 | 5 | 6 |
年产量y(万吨) | 6.6 | 6.7 | 7 | 7.1 | 7.2 | 7.4 |
(Ⅰ)根据表中数据,建立![]() 关于的线性回归方程
关于的线性回归方程![]() ;
;
(Ⅱ)根据线性回归方程预测2019年该地区该农产品的年产量.
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: ,
,![]() .(参考数据:
.(参考数据:![]() ,计算结果保留小数点后两位)
,计算结果保留小数点后两位)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() 、
、![]() ,点
,点![]() 在椭圆上,有
在椭圆上,有![]() ,椭圆的离心率为
,椭圆的离心率为![]() ;
;
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)已知![]() ,过点
,过点![]() 作直线
作直线![]() 与椭圆交于
与椭圆交于![]() 不同两点,线段
不同两点,线段![]() 的中垂线为
的中垂线为![]() ,线段
,线段![]() 的中点为
的中点为![]() 点,记
点,记![]() 与
与![]() 轴的交点为
轴的交点为![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 过点
过点![]() ,且圆心在直线
,且圆心在直线![]() 上.
上.
(1)求圆![]() 的方程;
的方程;
(2)平面上有两点![]() ,点
,点![]() 是圆
是圆![]() 上的动点,求
上的动点,求![]() 的最小值;
的最小值;
(3)若![]() 是
是![]() 轴上的动点,
轴上的动点,![]() 分别切圆
分别切圆![]() 于
于![]() 两点,试问:直线
两点,试问:直线![]() 是否恒过定点?若是,求出定点坐标,若不是,说明理由.
是否恒过定点?若是,求出定点坐标,若不是,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业对设备进行技术升级改造,为了检验改造效果,现从设备改造后生产的大量产品中抽取了100件产品作为样本,检测一项质量指标值,统计整理为如图所示的频率分布直方图:
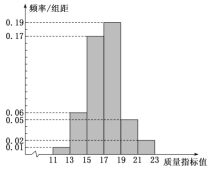
(1)估计该企业所生产产品的质量指标的平均数和中位数(中位数保留一位小数);
(2)若产品的质量指标在![]() 内,则该产品为残次品,生产并销售一件残次品该企业损失1万元;若产品的质量指标在
内,则该产品为残次品,生产并销售一件残次品该企业损失1万元;若产品的质量指标在![]() 范围内,则该产品为特优品,生产一件特优品该企业获利3万元.把样本中的残次品和特优品取出合并在一起,在从中任取2件产品进行销售,那么该企业收入为多少万元的可能性最大?
范围内,则该产品为特优品,生产一件特优品该企业获利3万元.把样本中的残次品和特优品取出合并在一起,在从中任取2件产品进行销售,那么该企业收入为多少万元的可能性最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,![]() 是由两个全等的菱形
是由两个全等的菱形![]() 和
和![]() 组成的空间图形,
组成的空间图形,![]() ,∠BAF=∠ECD=60°.
,∠BAF=∠ECD=60°.
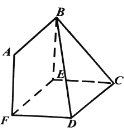
(1)求证:![]() ;
;
(2)如果二面角B-EF-D的平面角为60°,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于无穷数列{an},记T={x|x=aj﹣ai,i<j},若数列{an}满足:“存在t∈T,使得只要am﹣ak=t(m,k∈N*,m>k),必有am+1﹣ak+1=t”,则称数列具有性质P(t).
(1)若数列{an}满足![]() ,判断数列{an}是否具有性质P(2)?是否具有性质P(4)?说明理由;
,判断数列{an}是否具有性质P(2)?是否具有性质P(4)?说明理由;
(2)求证:“T是有限集”是“数列{an}具有性质P(0)”的必要不充分条件;
(3)已知{bn}是各项均为正整数的数列,且{bn}既具有性质P(2),又具有性质P(5),求证:存在正整数N,使得aN,aN+1,aN+2,…,aN+K,…是等差数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】点![]() 为
为![]() 所在的平面内,给出下列关系式:
所在的平面内,给出下列关系式:
①![]() ;
;
② ;
;
③![]() .
.
则点![]() 依次为
依次为![]() 的( )
的( )
A.内心、重心、垂心B.重心、内心、垂心C.重心、内心、外心D.外心、垂心、重心
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国是世界上严重缺水的国家,某市为了制定合理的节水方案,对居民用水情况进行调查,通过抽样,获得某年100为居民每人的月均用水量(单位:吨),将数据按照![]() 分成9组,制成了如图所示的频率分布直方图.
分成9组,制成了如图所示的频率分布直方图.
(1)求直方图的![]() 的值;
的值;
(2)设该市有30万居民,估计全市居民中月均用水量不低于3吨的人数,说明理由.
(3)估计居民月用水量的中位数.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com