
如图,矩形 所在的平面与正方形
所在的平面与正方形 所在的平面相互垂直,
所在的平面相互垂直, 是
是 的中点.
的中点.

(1)求证: ∥平面
∥平面 ;
;
(2)求证:平面 ⊥平面
⊥平面 .
.
(1)证明详见解析;(2)证明详见解析.
【解析】
试题分析:(1)要证线面平行,只须在平面内找到一条直线与这条直线平行,对本小题来说,连接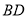 交
交 于点
于点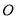 ,由三角形的中位线定理可证得
,由三角形的中位线定理可证得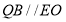 ,问题得证;(2)要证面面垂直,只要在其中一个平面内找到一条直线与另一个平面垂直即可,由四边形
,问题得证;(2)要证面面垂直,只要在其中一个平面内找到一条直线与另一个平面垂直即可,由四边形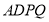 为正方形且
为正方形且 为对角线
为对角线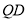 的中点,所以有
的中点,所以有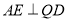 ,故可考虑证明
,故可考虑证明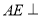 平面
平面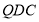 ,故需要在平面
,故需要在平面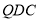 内再找一条直线与
内再找一条直线与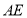 垂直即可,由平面
垂直即可,由平面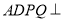 平面
平面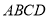 ,交线为
,交线为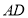 且
且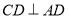 ,从而
,从而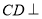 平面
平面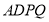 ,可得
,可得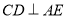 ,从而问题得证.
,从而问题得证.
试题解析:(1)连接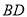 交
交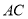 于
于 ,连接
,连接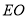

在三角形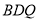 中,
中,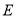 ,
, 分别为
分别为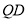 和
和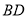 的中点
的中点
所以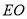 ∥
∥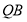 . 2分
. 2分
又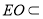 平面
平面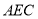 ,
,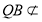 平面
平面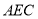
所以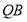 ∥平面
∥平面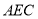 4分
4分
(2)因为矩形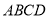 所在的平面与正方形
所在的平面与正方形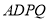 所在的平面相互垂直
所在的平面相互垂直
平面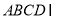 平面
平面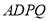 =
=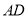 ,
,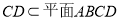 ,
,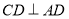
所以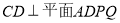
又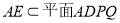 ,所以
,所以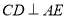 6分
6分
又因为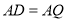 ,
,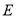 是
是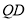 的中点,所以
的中点,所以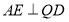
又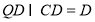 ,所以
,所以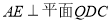 7分
7分
由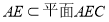 ,所以平面
,所以平面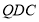 ⊥平面
⊥平面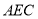 8分.
8分.
考点:1.线面平行的证明;2.面面垂直的判定与性质.


科目:高中数学 来源:2015届北京市西城区高二第一学期期末文科数学试卷(解析版) 题型:选择题
若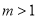 ,则方程
,则方程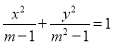 表示( )
表示( )
A. 焦点在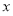 轴上的椭圆 B. 焦点在
轴上的椭圆 B. 焦点在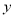 轴上的椭圆
轴上的椭圆
C. 焦点在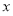 轴上的双曲线 D. 焦点在
轴上的双曲线 D. 焦点在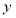 轴上的双曲线
轴上的双曲线
查看答案和解析>>
科目:高中数学 来源:2015届北京东城(南片)高二上学期期末考试文数学试卷(解析版) 题型:选择题
某学校高中部组织赴美游学活动,其中高一240人,高二260人,高三300人,现需按年级抽样分配参加名额40人,高二参加人数为
A. 12 B. 13 C. 14 D. 15
查看答案和解析>>
科目:高中数学 来源:2015届北京东城区高二第一学期期末考试理科数学试卷(解析版) 题型:选择题
 ,
, 是两个不重合的平面,在下列条件中,可判定
是两个不重合的平面,在下列条件中,可判定 ∥
∥ 的是( )
的是( )
A. ,
, 都与平面
都与平面 垂直
垂直
B. 内不共线的三点到
内不共线的三点到 的距离相等
的距离相等
C. ,
, 是
是 内的两条直线且
内的两条直线且 ∥
∥ ,
, ∥
∥
D. ,
, 是两条异面直线且
是两条异面直线且 ∥
∥ ,
, ∥
∥ ,
, ∥
∥ ,
,  ∥
∥
查看答案和解析>>
科目:高中数学 来源:2015届北京东城区高二第一学期期末考试文科数学试卷(解析版) 题型:选择题
已知 为椭圆
为椭圆 上的一点,
上的一点, ,
, 分别为椭圆的上、下顶点,若△
分别为椭圆的上、下顶点,若△ 的面积为6,则满足条件的点
的面积为6,则满足条件的点 的个数为( )
的个数为( )
A.0 B.2 C.4 D.6
查看答案和解析>>
科目:高中数学 来源:2015届云南玉溪一中高二上学期期末考试理科数学试卷(解析版) 题型:选择题
定义域为 的偶函数
的偶函数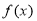 满足对
满足对 ,有
,有 ,且当
,且当 时,
时, ,若函数
,若函数 至少有三个零点,则
至少有三个零点,则 的取值范围是( )
的取值范围是( )
A. B.
B. C.
C.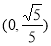 D.
D.
查看答案和解析>>
科目:高中数学 来源:2015届上海浦东新区高二上学期期末质量测试数学试卷(解析版) 题型:填空题
2013年12月初,上海遭遇最严重的雾霾天气,空气质量持续重度污染.某教室安装新型空气净化器,每小时可将 含量降低
含量降低 .该净化器连续工作 小时,可将
.该净化器连续工作 小时,可将 从
从 降到
降到 以下.(结果保留整数)
以下.(结果保留整数)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com