
【题目】已知圆![]() ,直线
,直线![]() 经过点A (1,0).
经过点A (1,0).
(1)若直线![]() 与圆C相切,求直线
与圆C相切,求直线![]() 的方程;
的方程;
(2)若直线![]() 与圆C相交于P,Q两点,求三角形CPQ面积的最大值,并求此时直线
与圆C相交于P,Q两点,求三角形CPQ面积的最大值,并求此时直线![]() 的方程.
的方程.
【答案】(1)![]() 或
或![]() (2)y=x-1或y=7x-7
(2)y=x-1或y=7x-7
【解析】试题分析:(1)由直线与圆相切可得圆心(3,4)到已知直线![]() 的距离等于半径2,设直线点斜式方程,列方程可得斜率,最后验证斜率不存在时是否满足条件(2)由垂径定理可得弦长PQ,而三角形的高为圆心到直线
的距离等于半径2,设直线点斜式方程,列方程可得斜率,最后验证斜率不存在时是否满足条件(2)由垂径定理可得弦长PQ,而三角形的高为圆心到直线![]() 的距离d,所以
的距离d,所以![]() ,利用基本不等式求最值可得当d=
,利用基本不等式求最值可得当d=![]() 时,S取得最小值2,再根据点到直线距离公式求直线
时,S取得最小值2,再根据点到直线距离公式求直线![]() 的斜率,即得
的斜率,即得![]() 的方程.
的方程.
试题解析:(1)①若直线![]() 的斜率不存在,则直线
的斜率不存在,则直线![]() ,符合题意.
,符合题意.
②若直线![]() 斜率存在,设直线
斜率存在,设直线![]() 为
为![]() ,即
,即![]() .
.
由题意知,圆心(3,4)到已知直线![]() 的距离等于半径2,
的距离等于半径2,
即![]() ,解得
,解得![]() ,
,
所求直线方程为![]() ,或
,或![]() ;
;
(2)直线与圆相交,斜率必定存在,且不为0,设直线方程为![]() ,
,
则圆心到直线![]() 的距离
的距离![]() ,
,
又∵三角形![]() 面积
面积
![]()
∴当d=![]() 时,S取得最小值2,则
时,S取得最小值2,则![]() ,
, ![]() ,
,
故直线方程为y=x-1,或y=7x-7.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】袋子中装有编号为![]() 的3个黑球和编号为
的3个黑球和编号为![]() 的2个红球,从中任意摸出2个球.
的2个红球,从中任意摸出2个球.
(Ⅰ)写出所有不同的结果;
(Ⅱ)求恰好摸出1个黑球和1个红球的概率;
(Ⅲ)求至少摸出1个红球的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2017年天猫五一活动结束后,某地区研究人员为了研究该地区在五一活动中消费超过3000元的人群的年龄状况,随机在当地消费超过3000元的群众中抽取了500人作调查,所得概率分布直方图如图所示:记年龄在![]() ,
, ![]() ,
, ![]() 对应的小矩形的面积分别是
对应的小矩形的面积分别是![]() ,且
,且![]() .
.
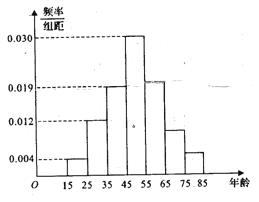
(1)以频率作为概率,若该地区五一消费超过3000元的有30000人,试估计该地区在五一活动中消费超过3000元且年龄在![]() 的人数;
的人数;
(2)计算在五一活动中消费超过3000元的消费者的平均年龄;
(3)若按照分层抽样,从年龄在![]() ,
, ![]() 的人群中共抽取7人,再从这7人中随机抽取2人作深入调查,求至少有1人的年龄在
的人群中共抽取7人,再从这7人中随机抽取2人作深入调查,求至少有1人的年龄在![]() 内的概率.
内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=ex-ax-2.
(1)求f(x)的单调区间;
(2)若a=1,k为整数,且当x>0时,(x-k)f′(x)+x+1>0,求k的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 的前n项和为Sn,点
的前n项和为Sn,点![]() 在直线
在直线![]() 上,数列
上,数列![]() 为等差数列,且
为等差数列,且![]() ,前9项和为153.
,前9项和为153.
(1)求数列![]() 、
、![]() 的通项公式;
的通项公式;
(2)设![]() ,数列
,数列![]() 的前n项和为
的前n项和为![]() ,求使不等式
,求使不等式![]() 对一切的
对一切的![]() 都成立的最大整数k.
都成立的最大整数k.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了参加师大附中第30届田径运动会的开幕式,高三年级某6个班联合到集市购买了6根竹竿,作为班期的旗杆之用,它们的长度分别为3.8,4.3,3.6,4.5,4.0,4.1(单位:米).
(1)若从中随机抽取两根竹竿,求长度之差不超过0.5米的概率;
(2)若长度不小于4米的竹竿价格为每根10元,长度小于4米的竹竿价格为每根![]() 元.从这6根竹竿中随机抽取两根,若期望这两根竹竿的价格之和为18元,求
元.从这6根竹竿中随机抽取两根,若期望这两根竹竿的价格之和为18元,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C的两个焦点分别为![]() ,且椭圆C过点P(3,2).
,且椭圆C过点P(3,2).
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)与直线OP平行的直线交椭圆C于A,B两点,求△PAB面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com