Question

13．甲船在A处遇险，在甲船正西南10海里B处的乙船收到甲船的报警后，测得甲船是沿着方位角105°的方向，以每小时9海里的速度向某岛靠近．如果乙船要在40分钟内追上甲船，则乙船应以多少速度并沿什么方向航行？

Answer 1

分析 通过画出图象，设乙船速度为ν海里/小时，在C处追上甲船，在△ABC中利用余弦定理可知ν=21，利用正弦定理可知sin∠B=$\frac{3\sqrt{3}}{14}$，进而计算可得结论．

解答 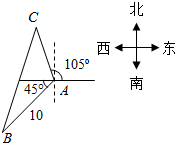解：如图，设乙船速度为ν海里/小时，在C处追上甲船，
∠BAC=45°+180°-105°=120°，
在△ABC中，由余弦定理得：BC²=AC²+AB²-2AC•AB•cos∠BAC，
即$（\frac{2}{3}v）^{2}$=$（\frac{2}{3}×9）^{2}$+10²-2×$\frac{2}{3}$×9×10×cos120°，
整理得：ν=21，
又由正弦定理可知：$\frac{BC}{sin∠BAC}$=$\frac{AC}{sin∠B}$，
∴sin∠B=$\frac{AC•sin∠BAC}{BC}$=$\frac{\frac{2}{3}×9}{\frac{2}{3}×21}$×sin∠120°=$\frac{3\sqrt{3}}{14}$，
∴B≈21°47′，
即乙船应按东偏北45°+21°47′=66°47′的角度、以21海里/小时的速度航行．

点评 本题考查解三角形的应用，考查数形结合能力，注意解题方法的积累，属于中档题．