
【题目】已知函数![]() .
.
(1)求函数![]() 的最小正周期及单调增区间;
的最小正周期及单调增区间;
(2)当![]() 时,求函数
时,求函数![]() 的最大值及最小值.
的最大值及最小值.
【答案】(1)周期![]() ,增区间为
,增区间为![]() (2)最大值为
(2)最大值为![]() ,最小值为-1
,最小值为-1
【解析】
(1)找出函数f(x)解析式中的ω的值,代入周期公式即可求出函数的最小正周期,由正弦函数的单调递增区间[2kπ![]() ,2kπ
,2kπ![]() ]列出关于x的不等式,求出不等式的解集即为函数的单调递增区间;
]列出关于x的不等式,求出不等式的解集即为函数的单调递增区间;
(2)由x的范围,求出2x![]() 的范围,根据正弦函数的图象与性质可得2x
的范围,根据正弦函数的图象与性质可得2x![]() 为
为![]() 时,f(x)取得最大值,当2x
时,f(x)取得最大值,当2x![]() 为
为![]() 时函数f(x)取得最小值,分别求出最大值和最小值即可.
时函数f(x)取得最小值,分别求出最大值和最小值即可.
(1)f(x)![]() sin(2x
sin(2x![]() ),
),
∵ω=2,∴最小正周期T![]() π,由2kπ
π,由2kπ![]() 2x
2x![]() 2kπ
2kπ![]() (k∈Z),
(k∈Z),
解得kπ![]() x≤kπ
x≤kπ![]() (k∈Z),
(k∈Z),
故函数f(x)的单调增区间是[kπ![]() ,kπ
,kπ![]() ](k∈Z);
](k∈Z);
(2)当x∈[![]() ,
,![]() ]时,(2x
]时,(2x![]() )∈[
)∈[![]() ,
,![]() ],
],
故当2x![]() ,即x
,即x![]() 时,f(x)有最大值
时,f(x)有最大值![]() ,
,
当2x![]() ,即x
,即x![]() 时,f(x)有最小值﹣1.
时,f(x)有最小值﹣1.


 特高级教师点拨系列答案
特高级教师点拨系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() (
(![]() )的离心率为
)的离心率为![]() ,且a2=2b.
,且a2=2b.
(1)求椭圆的方程;
(2)直线l:x﹣y+m=0与椭圆交于A,B两点,是否存在实数m,使线段AB的中点在圆x2+y2=5上,若存在,求出m的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于函数 ,下列
,下列![]() 个结论正确的是__________(把你认为正确的答案全部写上).
个结论正确的是__________(把你认为正确的答案全部写上).
(1)任取![]() ,都有
,都有![]() ;
;
(2)函数![]() 在
在![]() 上单调递增;
上单调递增;
(3)![]() ,对一切
,对一切![]() 恒成立;
恒成立;
(4)函数![]() 有
有![]() 个零点;
个零点;
(5)若关于![]() 的方程
的方程![]() 有且只有两个不同的实根
有且只有两个不同的实根![]() ,
,![]() ,则
,则![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】箱子里有16张扑克牌:红桃![]() 、
、![]() 、4,黑桃
、4,黑桃![]() 、8、7、4、3、2,草花
、8、7、4、3、2,草花![]() 、
、![]() 、6、5、4,方块
、6、5、4,方块![]() 、5,老师从这16张牌中挑出一张牌来,并把这张牌的点数告诉了学生甲,把这张牌的花色告诉了学生乙,这时,老师问学生甲和学生乙:你们能从已知的点数或花色中推知这张牌是什么牌吗?于是,老师听到了如下的对话:学生甲:我不知道这张牌;学生乙:我知道你不知道这张牌;学生甲:现在我知道这张牌了;学生乙:我也知道了.则这张牌是( )
、5,老师从这16张牌中挑出一张牌来,并把这张牌的点数告诉了学生甲,把这张牌的花色告诉了学生乙,这时,老师问学生甲和学生乙:你们能从已知的点数或花色中推知这张牌是什么牌吗?于是,老师听到了如下的对话:学生甲:我不知道这张牌;学生乙:我知道你不知道这张牌;学生甲:现在我知道这张牌了;学生乙:我也知道了.则这张牌是( )
A. 草花5B. 红桃![]()
C. 红桃4D. 方块5
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“有黑扫黑、无黑除恶、无恶治乱”,维护社会稳定和和平发展.扫黑除恶期间,大量违法分子主动投案,某市公安机关对某月连续7天主动投案的人员进行了统计,![]() 表示第
表示第![]() 天主动投案的人数,得到统计表格如下:
天主动投案的人数,得到统计表格如下:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 3 | 4 | 5 | 5 | 5 | 6 | 7 |
(1)若![]() 与
与![]() 具有线性相关关系,请根据上表提供的数据,用最小二乘法求出
具有线性相关关系,请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)判定变量![]() 与
与![]() 之间是正相关还是负相关.(写出正确答案,不用说明理由)
之间是正相关还是负相关.(写出正确答案,不用说明理由)
(3)预测第八天的主动投案的人数(按四舍五入取到整数).
参考公式: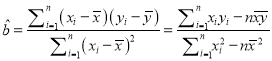 ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】农科院的专家为了了解新培育的甲、乙两种麦苗的长势情况,从种植有甲、乙两种麦苗的两块试验田中各抽取6株麦苗测量株高,得到的数据如下(单位:![]() ):
):
甲:9,10,11,12,10,20
乙:8,14,13,10,12,21
(1)用茎叶图表示这些数据:
(2)分别计算两组数据的中位数、平均数与方差,并由此估计甲、乙两种麦苗株高的平均数及方差.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列结论:
①若![]() 为真命题,则
为真命题,则![]() 、
、![]() 均为真命题;
均为真命题;
②命题“若![]() ,则
,则![]() ”的逆否命题是“若
”的逆否命题是“若![]() ,则
,则![]() ”;
”;
③若命题![]() ,
,![]() ,则
,则![]() ,
,![]() ;
;
④“![]() ”是“
”是“![]() ”的充分不必要条件.其中正确的结论有____.
”的充分不必要条件.其中正确的结论有____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com