
【题目】农科院的专家为了了解新培育的甲、乙两种麦苗的长势情况,从种植有甲、乙两种麦苗的两块试验田中各抽取6株麦苗测量株高,得到的数据如下(单位:![]() ):
):
甲:9,10,11,12,10,20
乙:8,14,13,10,12,21
(1)用茎叶图表示这些数据:
(2)分别计算两组数据的中位数、平均数与方差,并由此估计甲、乙两种麦苗株高的平均数及方差.
【答案】(1)答案见解析;(2)两组数据中甲种麦苗株高的中位数为![]() ,平均数为12,方差为
,平均数为12,方差为![]() ;乙种麦苗株高的中位数为
;乙种麦苗株高的中位数为![]() ,平均数为13,方差为
,平均数为13,方差为![]() ;由此估计甲种麦苗株高的平均数为12,方差为
;由此估计甲种麦苗株高的平均数为12,方差为![]() ,乙种麦苗株高的平均数为13,方差为
,乙种麦苗株高的平均数为13,方差为![]() .
.
【解析】
(1)直接由已知数据画茎叶图即可;
(2)由于每组有6个数,所以中位数为最中间两个数的平均数,平均数和方差直接利用公求解,然后利用样本估计总体的情况
解:(1)茎叶图如图所示
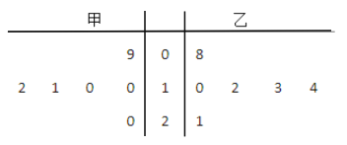
(2)甲种麦苗株高的中位数![]()
甲种麦苗株高的平均数![]()
甲种麦苗株高的方差
![]()
乙种麦苗株高的中位数![]()
乙种麦苗株高的平均值![]()
乙种麦苗株高的方差
![]()
由此估计甲种麦苗株高的平均数为12,方差为![]() ,
,
乙种麦苗株高的平均数为13,方差为![]()


科目:高中数学 来源: 题型:
【题目】已知球O是正三棱锥(底面为正三角形,顶点在底面的射影为底面中心)A-BCD的外接球,BC=3,![]() ,点E在线段BD上,且BD=3BE,过点E作圆O的截面,则所得截面圆面积的取值范围是__.
,点E在线段BD上,且BD=3BE,过点E作圆O的截面,则所得截面圆面积的取值范围是__.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).以坐标原点为极点,
为参数).以坐标原点为极点,![]() 轴的非负半轴为极轴建立极坐标系,曲线
轴的非负半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)将![]() 的方程化为普通方程,将
的方程化为普通方程,将![]() 的方程化为直角坐标方程;
的方程化为直角坐标方程;
(Ⅱ)已知直线![]() 的参数方程为
的参数方程为![]() ,
,![]() 为参数,且
为参数,且![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,且
,且![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有一个关于平面图形的命题:如图,同一平面内有两个边长都是2的正方形,其中一个的某顶点在另一个的中心,则这两个正方形重叠部分的面积恒为______.
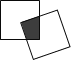
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 是平行四边形
是平行四边形![]() 所在平面外一点,如果
所在平面外一点,如果![]() ,
,![]() ,
,![]() .(1)求证:
.(1)求证:![]() 是平面
是平面![]() 的法向量;
的法向量;
(2)求平行四边形![]() 的面积.
的面积.
【答案】(1)证明见解析;(2)![]() .
.
【解析】试题分析:
(1)由题意结合空间向量数量积的运算法则计算可得![]() ,
,![]() .则
.则![]() ,
,![]() ,结合线面垂直的判断定理可得
,结合线面垂直的判断定理可得![]() 平面
平面![]() ,即
,即![]() 是平面
是平面![]() 的法向量.
的法向量.
(2)利用平面向量的坐标计算可得![]() ,
,![]() ,
,![]() ,则
,则![]() ,
,![]() ,
,![]() .
.
试题解析:
(1)∵![]() ,
,
![]() .
.
∴![]() ,
,![]() ,又
,又![]() ,∴
,∴![]() 平面
平面![]() ,
,
∴![]() 是平面
是平面![]() 的法向量.
的法向量.
(2)∵![]()
![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
故![]() ,
,![]()
![]() .
.
【题型】解答题
【结束】
19
【题目】(1)求圆心在直线![]() 上,且与直线
上,且与直线![]() 相切于点
相切于点![]() 的圆的方程;
的圆的方程;
(2)求与圆![]() 外切于点
外切于点![]() 且半径为
且半径为![]() 的圆的方程.
的圆的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国是世界上严重缺水的国家,某市为了制定合理的节水方案,对居民用水情况进行调查,通过抽样,获得某年100为居民每人的月均用水量(单位:吨),将数据按照![]() 分成9组,制成了如图所示的频率分布直方图.
分成9组,制成了如图所示的频率分布直方图.
(1)求直方图的![]() 的值;
的值;
(2)设该市有30万居民,估计全市居民中月均用水量不低于3吨的人数,说明理由.
(3)估计居民月用水量的中位数.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com